CS 76
Adversarial search
Professor Devin Balkcom
devin@cs.dartmouth.edu
office: Sudikoff 206
Notes
- AIMA, chapters 5.4, 5.5, 5.7.
- Blind robot, polynomial time
Adversarial search
My happiness, your expense: I win (+1), you lose (-1).
- Initial state
- Successor function
- Terminal test
- Utility function. (e.g., +1, 0, -1).
Basic case: zero-sum, deterministic, perfect-information, 2-player games.
XKCDTic-tac-toe
Max will play x's, and Min will play o's.
- terminal states: states for which the game is over
- shared utility function. But Min wants to minimize it.
Some terminal states:
Non-terminal states
With optimal play, every state has a fixed utility.
Minimax search
Minimax search
Min gets last move.
Minimax search
Min gets last move.
Minimax search
Min gets last move.
Minimax search
Max gets the move prior to the last move.
Minimax search
Optimal values, assuming two optimal players.
Can Max do better if Min is not optimal?
Alpha-beta pruning
Alpha-beta pruning
Alpha-beta pruning
Alpha-beta pruning
Alpha-beta pruning
Alpha-beta pruning
What if we'd gotten a 2 before the 14? Order matters!
Heuristic evaluation

(Photo by Cburnett, Wikipedia.)
material: pawn 1, bishop 3, rook 4, queen 8, king ???
Cutoff tests
Horizon effects are a problem: stalling tactics can push bad states beyond the depth searched.
Quiescent states are good candidates for cutoff.
Perhaps search slightly deeper, along captures to determine quiescence? Or a single best move each time.
Iterative deepening
- Need to make a move when time is up.
- alpha-beta needs to know cutoff depth and complete all work
- The game tree is a tree (but also, transposition table)
Other tricks
- Forward pruning
- Null move heuristic
- Zobrist hashing
Null-move heuristic
Assume current player forfeits turn. If position still quite strong, a very strong position indeed.
- Do a shallow alpha-beta search on a subtree, with null-move at root.
- If still good, other player should avoid subtree.
- Forward prune, or treat result as upper bound on node for the player who got to move twice.
Zobrist hashing
Transposition table: avoid re-visiting states in search.
Problems with letting Java just hash that object:
- Memory: too many states to store objects in buckets.
- Speed. More speed = more depth = win.
(51% of the vote in an election.)
So we need a fast hash function and we won't store objects -- just hope for limited collisions.
Zobrist hashing
- Decompose the state.
In chess, each location can have one of 12 pieces or none. White pawn at 4, 2 is one component of the state. Black rook at 2, 6 is another component. - For each component, pick a random bitstring.
For chess, 64 * 13 = 832 random bitstrings. - Build a hash by XORing bitstrings for components.
At the beginning, 1a white rook, 1b white knight, ... - To get a new hash, XOR with parent hash.
- Store true or a cost for move reordering.
- Maybe an array for the table. 64-bit indices?
Uncertainty
Some sources:
- Lack of computation time (chess)
- Lack of prediction power (dice, shuffling)
- Lack of knowledge (hidden cards)
Dice games
Max moves, then chance, then Min moves, then chance. In Backgammon, dice are rolled to give available moves.
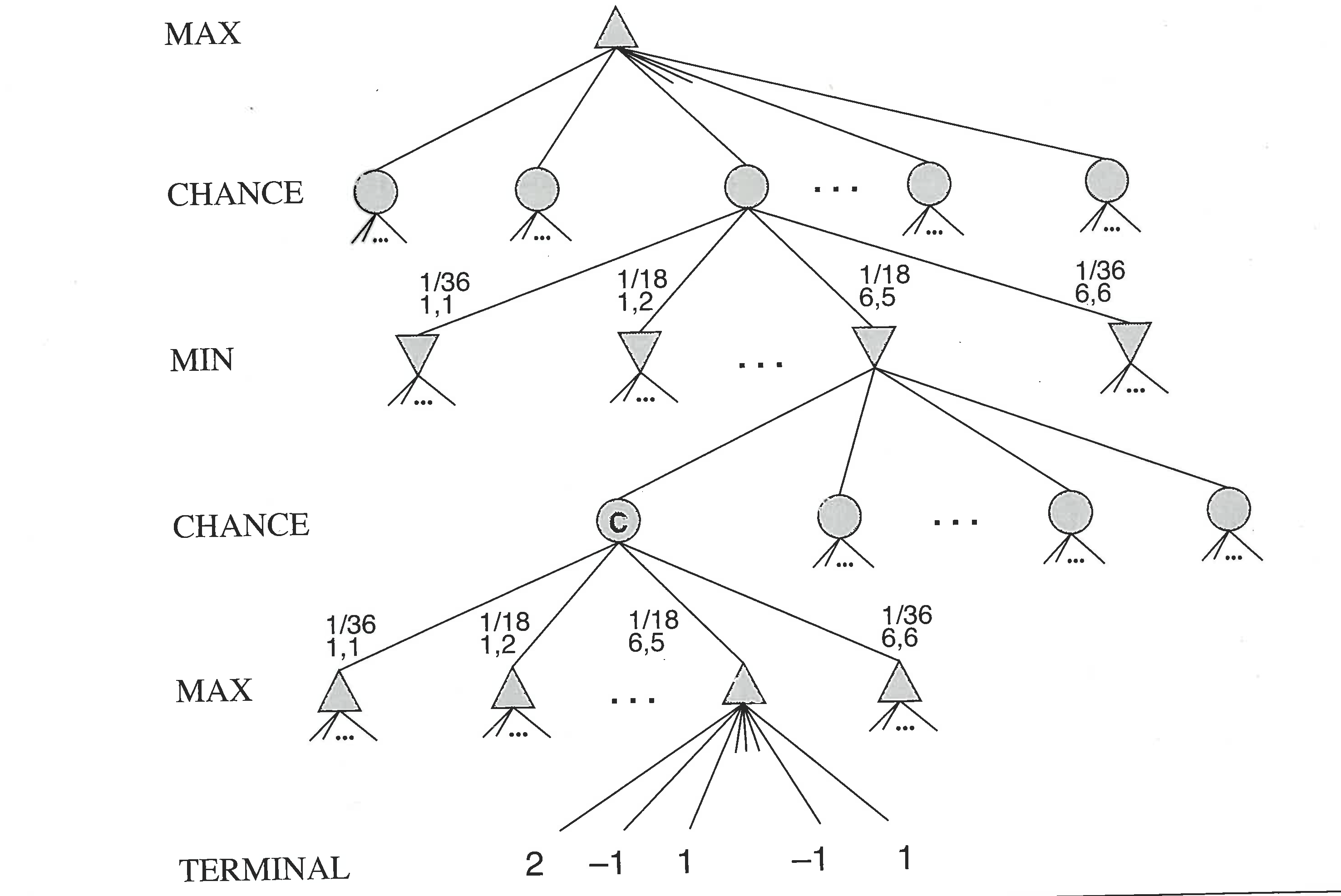
Dice games
Expectiminimax can compute the expected value of any node: value of sum of the known values for the terminal node.
Assumes values are actual utilities and that humans maximize expected value -- if that were true, Sheldon Adelson would not be so rich.
Technical problems: computation and modeling.
Dice games
In deterministic games, only order matters. But now:
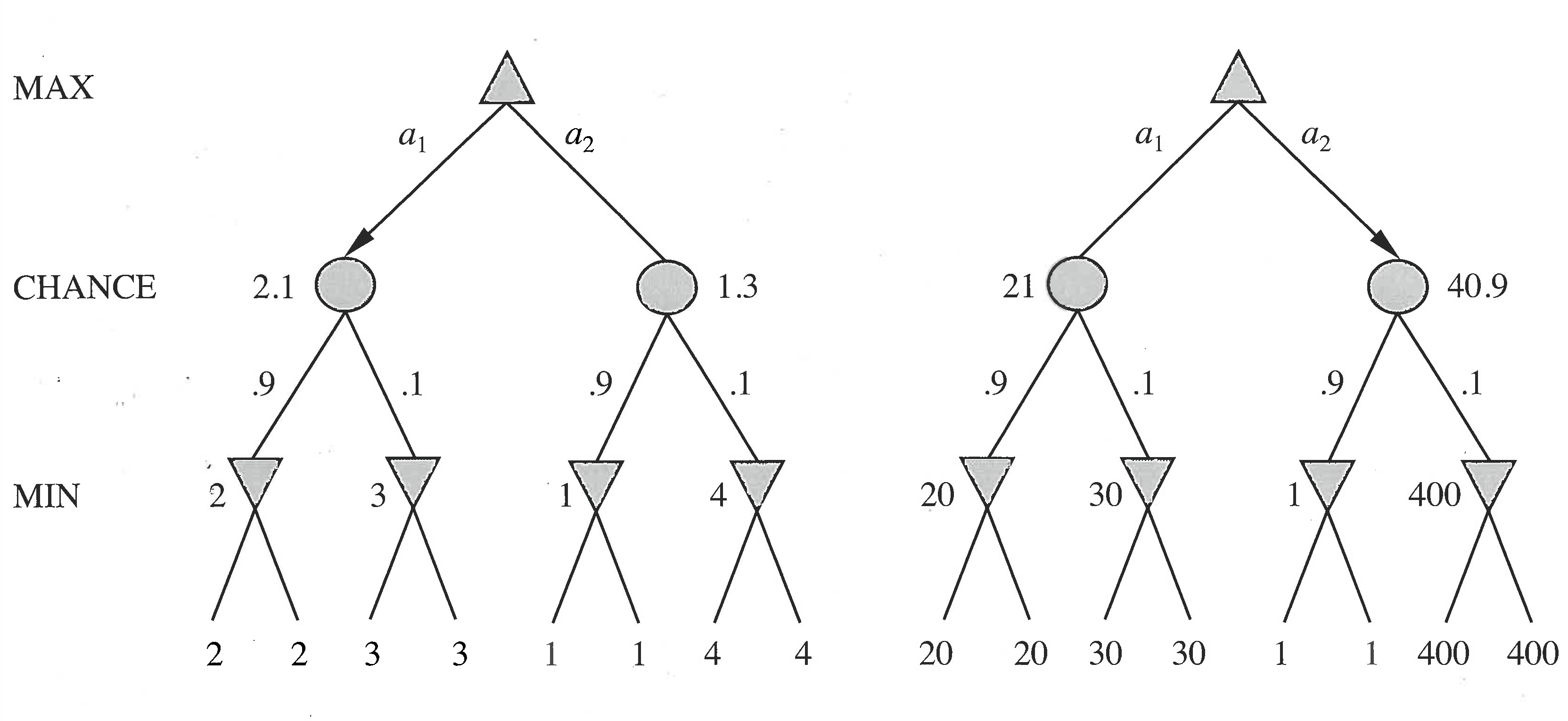
An order-preserving transformation changes actions.
Card games
Cards dealt randomly at the start of the match.
Bad approach:
- For each possible state after deal, compute optimal strategy.
- Then value each move based on relative value over all possible states.
Problems:
- A lot of start states. Alpha-beta over each?
- You don't know what state you are in!
Information matters
Mondays:
- Road A leads to 1 gold. Road B leads to a fork.
- Go left from the fork, 100 gold. Go right, die.
- Optimal strategy: B
Tuesdays:
- Road A leads to 1 gold. Road B leads to a fork.
- Go left from the fork, die. Go right, 100 gold.
- Optimal strategy: B
I can't remember what day it is. Choose B?
Non-zero sum games
Oderint, dum metuant. (Lucius Accius)
Prisoner's dilemma:
| B Co-op | B Defect | |
|---|---|---|
| A Co-op | (-1, -1) | (-9, 0) |
| A Defect | (0, -9) | (-6, -6) |
payoff(A) + payoff(B) different for each outcome
Is it possible to co-operate to raise both payoffs?
Normal form
Each of $n$ players has:
- A strategy space, $S_i$, available actions
- A payoff function: takes $n$ strategies, returns utility
Example:
- $S_1 = \{c, d\}$, $S_2 = \{c, d\}$
- $u_1(c, c) = -1$
- $u_1(c, d) = -9$
- ...
Strict domination
Some strategies are better for me than others
no matter what you do.
| B Co-op | B Defect | |
|---|---|---|
| A Co-op | (-1, -1) | (-9, 0) |
| A Defect | (0, -9) | (-6, -6) |
- A can get 0 (vs -1) by defecting if B cooperates.
- A can get -6 (vs -9) by defecting if B defects.
Discussion: repeated games
Assume we intend to play 20 games. Assume both players agree to play the following strategy:
Punishment: I will cooperate, until you do not. If you defect on one round, I will take revenge for one turn by defecting, and then go back to cooperating.
Is this strategy believable? (Do I believe your threat? Do we cooperate?)
Discussion: repeated games
Assume we intend to play 20 games. Assume both players agree to play the following strategy:
Grim trigger: I will cooperate, until you do not. If you defect on one round, I will take revenge for all remaining rounds, and defect each time.
Is this strategy believable? (Do I believe your threat? Do we cooperate?)
Repeated games
Grim trigger strategy: I'll cooperate until you defect. Then I will hate you and defect until the game ends.
- Is my threat credible?
- Cooperation possible if the game ends after 20 turns?
Is your cooperation credible, ever? (Propagation of horizon effects.)
Infinite horizon games
Is payoff infinite? How do we compare infinities?
Discount factor models possibility that game will end at some time, but we don't know when.
Cooperation is possible!