CS 76 / 176
Constraint satisfaction
Professor Devin Balkcom
devin@cs.dartmouth.edu
office: Sudikoff 206
Constraint satisfaction

Sometimes for a search probem:
- state can be factored (like Zobrist).
- path to solution does not matter.
CSP definition
(An example of factoring state.)
- $n$ variables: $X_1 \ldots X_n$
- For each variable, a domain $D_i$ of possible values.
Example: $D_1: X_1 \in {v_1, v_2, v_3}$ - $m$ constraints $C_1 \ldots C_m$, each specifiying allowable combinations of values for some set of variables.
An assigment of values to variables is the state of the problem. We want to find an assignment consistent with the constraints.
Map coloring
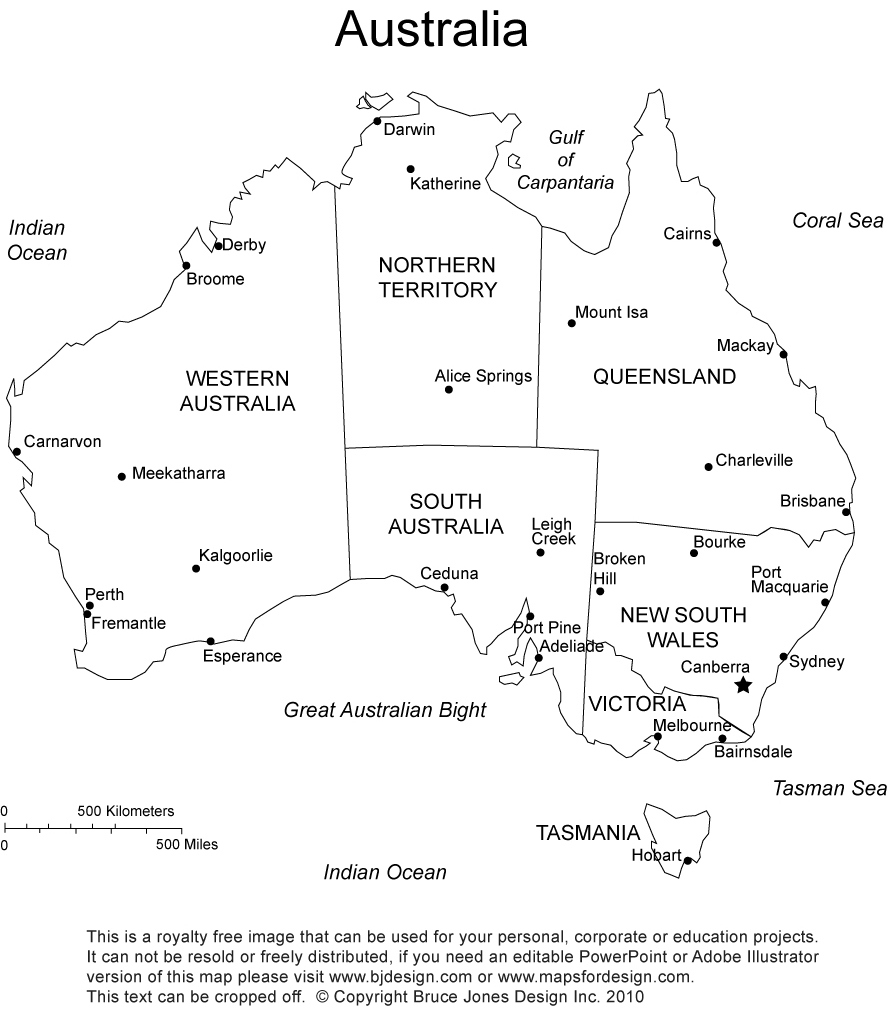
Map coloring
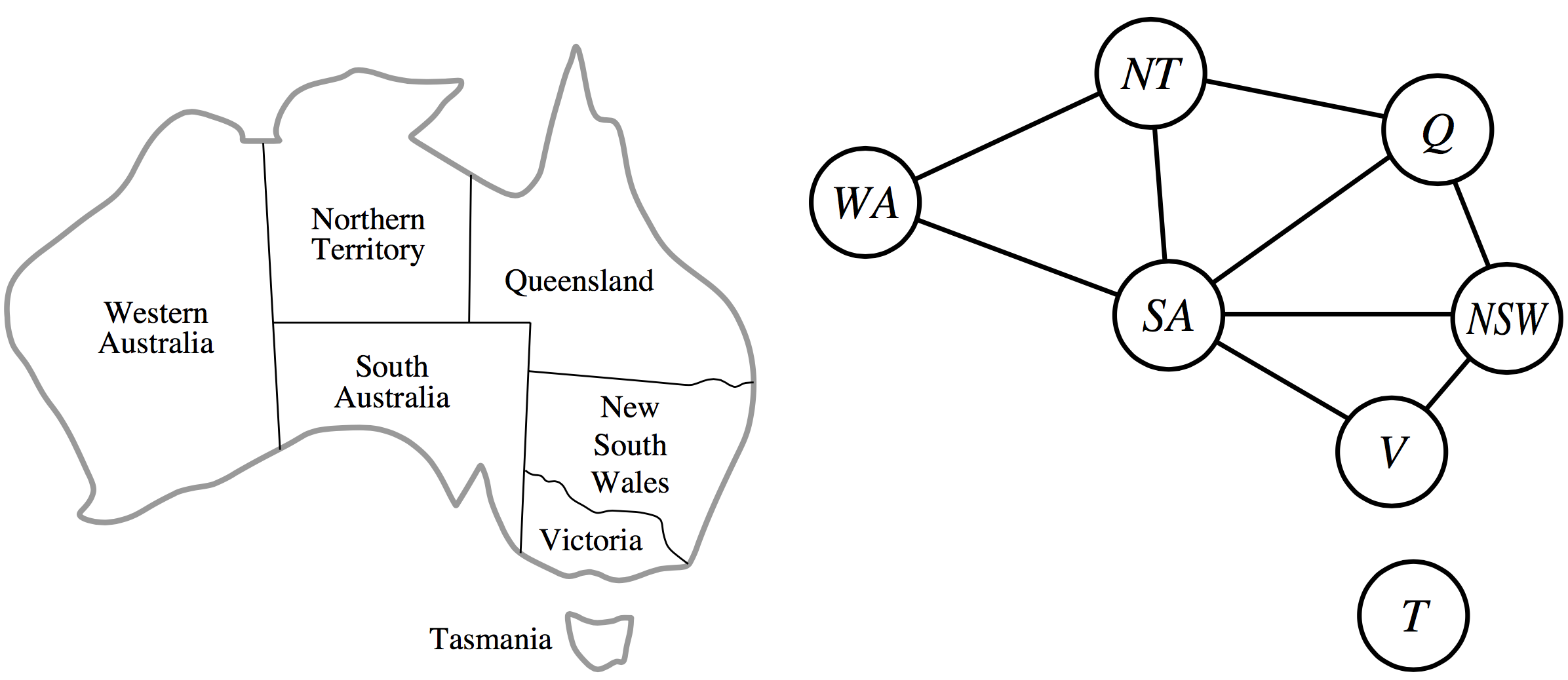
- Variables: $WA$, $NT$, $SA$, $Q$, $NSW$, $V$, $T$
- Domains: $D_i: {r, g, b}$
Constraints:
- $(WA, NT) \in \{(r, g), (r, b), (g, r), (g, b), (b, r), (b, g)\}$
- $(NT, SA) \in \{(r, g), (r, b), (g, r), (g, b), (b, r), (b, g)\}$
- ...
CSP definition
(An example of factoring state.)
- $n$ variables: $X_1 \ldots X_n$
- For each variable, a domain $D_i$ of possible values.
Example: $D_1: X_1 \in {v_1, v_2, v_3}$ - $m$ constraints $C_1 \ldots C_m$, each specifiying allowable combinations of values for some set of variables.
An assigment of values to variables is the state of the problem. We want to find an assignment consistent with the constraints.
Examples
(A quick list -- discussion coming soon.)
- Map coloring
- 8-queens
- Scheduling (job shops, section leader assignments, experiments/ observations with the Hubble.)
- Placing components on chips
- Continuous case: linear programs, mechanical stability, etc
Discussion: CSP formulations
What are variables, domains, constraints for each of the following?
- 8-queens
- section/ leader assignments to section times for CS 1
- Placing components on chips
Implementation notes
Variables have different names. But we want to write general code. An example assignment:
state = {0, 1, 1, 2, 0, 1, 0}
variable order: WA, NT, SA, Q, NSW, V, T
So NT has the value 1 (green).
Domains can be represented by sets of numbers.
Solution techniques
- Brute force
- Inference
- Clever search
- Random walk
Brute force CSP
- Variables: $WA$, $NT$, $SA$, $Q$, $NSW$, $V$, $T$
- Domains: $D_i: {r, g, b}$
Constraints:
- $(WA, NT) \in \{(r, g), (r, b), (g, r), (g, b), (b, r), (b, g)\}$
- $(NT, SA) \in \{(r, g), (r, b), (g, r), (g, b), (b, r), (b, g)\}$
- ...
- state = {0, 0, 0, 0, 0, 0, 0}? Nope.
- state = {0, 0, 0, 0, 0, 0, 1}? Nope.
- state = {0, 0, 0, 0, 0, 0, 2}? Nope.
- state = {0, 0, 0, 0, 0, 1, 0}? Nope.
- ...
Inference
Arc consistency
- Separate each constraint into two directed arcs.
- Store a current domain for each variable.
- Choose some partial assignment (possibly).
- Infer something to update domains.
We say that an arc from variable $X$ to variable $Y$ is consistent if for every value of $X$ there exists some value of $Y$.
Arc consistency
Assume $SA \in \{blue\}$ and $NSW \in \{red, blue\}$.
Is SA arc consistent with respect to NSW?
Yes, since for every value of SA (only blue), there is at least one value of NSW (in this case, red).
So, SA is consistent, and not causing any trouble.
Arc consistency
Assume $SA \in \{blue\}$ and $NSW \in \{red, blue\}$.
Is NSW arc consistent with respect to SA?
No, since for at least one value of NSW (blue), there are no legal values for $SA$.
i.e., we have learned something about NSW domain.
Delete blue from NSW domain.
Inference example

Let's use inference to quickly solve the map-coloring problem for Australia. (On the board.) Start with partial assignment $WA = red$.
AC-3 algorithm
- Add all arcs to a queue
- Pop an arc; enforce consistency
(delete values from domain of A if no legal values in B) - Add all arcs pointing to A to queue, if any deletions.
Run-time:
- $d$ values in domain. No arc added more than $d$ times.
- $c$ constraints, so $2c$ arcs, so $d \cdot 2c$ checks.
- Each check, for each value, check all adjacent values, $d^2$ time.
$O(c d^2)$
Generalized consistency
To make constraints consistent, delete values.
Generalized consistency
But consider the 'mega-variable' (SA, V), with possible assignments $(red, blue)$ and $(blue, red)$, after checking binary constraints and deleting.
Generalized consistency
Is $(red, blue)$ 3-consistent with any value from NSW domain? No, so delete $(red, blue)$ from the `SA-V` domain.
Same for $(blue, red)$.
Generalized consistency
What's the run-time? How about for higher-order consistency? (Consider brute-force assignment checking for $n$-consistency.)
Global constraints
What if each variable must have a different value? For example, a section for CS 1 must have its own room and cannot share.
One idea: Does an assignment of values to a set of variables cover a number of values equal to the number of variables in the set? (Written as code, not a white-list.)
Solving CSP by search
Naive approach:
- Choose a variable, assign a value.
- If no assignments possible without violating a constraint, backtrack by unassigning most recent value, make a different choice. (Basic DFS.)
Run-time. Branching factor at top is $n d$, if $d$ size of domain. At next level, $(n - 1) d$, since once variable has been assigned.
Tree has $n! d^n$ leaves. That can't be good; there are only $d^n$ possible assignments!
Order doesn't matter
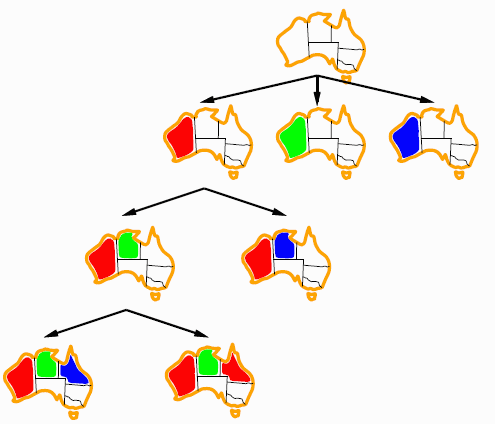
Consider only a single variable at each node.
Order doesn't matter

Branching factor is now $d$, depth $n$. So, $d^n$ leaves.
Order does matter
Ordering heuristics:
- Reordering variables might help
- Reordering values might help
Minimum remaining values

Assume we've assigned $WA = r$ and $NT = g$. Should we consider $SA$ next or $Q$ next?
- $Q \in \{b, r \}$
- $SA \in \{b\}$ bogus assignment $\Rightarrow$ "fail fast", good!
Degree heuristic

Pick variable involved in the most constraints: SA.
(Idea: get maximum information from first assigments.)
Value ordering
Idea: We don't have to try all values. Try the ones that are most promising first.
Least-constraining value: choose the value that rules out as few values for adjacent variables as possible.
Why fail-fast for variables, but fail-slow for values?
Interleaving
We can interleave search and inference.
Forward checking: Whenever variable X is assigned, delete conflicting values from adjacent domains.
or
Constraint propagation: create a queue, add arcs pointing to X, and propagate constraint using AC-3, etc.
Local search
min-conflicts:
- Choose a random conflicted variable
- Choose a value that violates the fewest constraints
- Loop
This works surprisingly well, particularly if there are many densely distributed solutions.
Which CSPs are hard, and which are easy?
Protein structure
Some apparently continuous CSP problems are not:
Assume we know all of the distances. Can we compute the configuration of the protein?
What if we don't know which atoms the distances correspond to? Variables $\theta_1 \ldots \theta_n$. Assign values so that distances appear in from legal set.
Continuous CSPs
Linear programs are one example.
- Choose values for variables $x_1, x_2, x_3, \ldots$
- Satisfying constraints of the form $a_1 x_1 + a_2 x_2 + a_3 x_3 + \ldots \le b_1$,
$a_1 x_1 + a_2 x_2 + a_3 x_3 + \ldots \le b_2$
Structural stability

Will it fall? (Image from Anne Loomis M.S. thesis.)
Structural stability
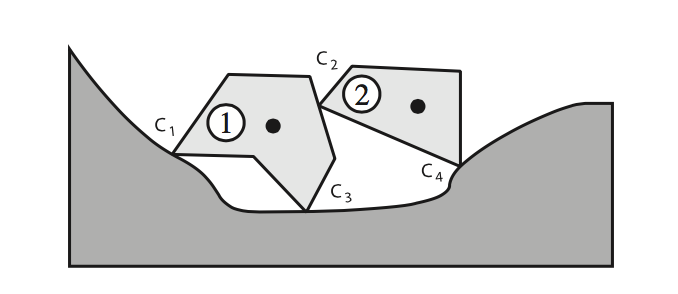
- Forces must be qual and opposite at each contact
- Sum of forces on each block zero, or collapses
- Contact forces are variables
Disassembling rubble

Which order should we take this apart in? (Jenga)
Disassembling rubble
Robot grasping
Reauleax's graphical method:
We want there to be no solution to some linear program.
CSP dual problems

For any CSP, we can pose a dual problem that has the same solution, and for which all constraints are binary.
CSP dual problems
- Choose the constraints of the primal as variables.
(Edges of constraint graph are now variables). - The values are combinations of values for primal problem that satisfy original constrants.
$(WA, NT) = C_1 \in \{ (r, g), (r, b), \ldots \}$
- New contraints: each pair of variables $C_i, C_j$ must agree on primal values if they share a variable in the primal problem.
$C_{12}: ((WA, NT), (WA, SA) ) \in \{ (rg, rb), (gr, gb), (br, bg) \}$
Why use the dual?
- Constraints are binary.
New constraints force edges of original constraint graph agree on values at vertices. If you make two constraints agree on red at a vertex, and then a third agrees with one of the others, they all agree.
- Sometimes the dual is simpler. (Join trees)
- Primal/dual algorithms work on both problems in alternation, and are state of the art for linear programming, quadratic programming.