CS 76 / 176

Outline of the next topics

• Uniform-cost search
• Mazeworld
• Informed search (heuristics)
• Greedy search
• A* search (on a tree)
• Deriving heuristics

Uniform cost search

Almost BFS, but uses priority queue for frontier.
(See figure 3.14 in the book.)

Priority queue:

• A0
• (pop A0, push B1, C4)
• B1 C4
• (pop B1, push D2)
• D2 C4
• (pop D2, push E3)
• E3 C4
• (Pop E3, goal found!)

Goal-test location in code

Priority queue:

• A0
• (pop A0, push B1, C4?)
• B1 C4
• (pop B1, push C2)
• C2
• (pop C2, goal found!)

Modifying priorities

There is a problem:

if child.state is in frontier with higher path-cost
  replace that frontier node with child

Priority queue:

• A0
• B1 C4
• C2 D4
• E3 D4

How do you efficiently check if a node is in a priority queue, or replace it efficiently?

Modifying priorities

• Fibonacci heap?
• Mark expensive item as removed, add cheaper item.

Replace explored set with explored dictionary, storing cost of least-expensive route to node as value. If a state is being considered for addition to the frontier, check if it is in explored already. If not, add to frontier. If so, but the new node has a less expensive path cost, change the cost in explored and add the new node anyway. Otherwise, do not add the node to the frontier.

Mazeworld

Robot can move N, S, E, W onto empty squares.

Mazeworld

Bi-directional BFS works.

Wavefront BFS

Or you can use a modified wavefront BFS.

Wavefront BFS

Skip Node data structure, store costs in an array.

Wavefront BFS

Queue contains coordinates of next squares to explore.

Wavefront BFS

And you don't need a visited set (it's implicit).

Wavefront BFS

No backchaining; do gradient descent on value function.

Wavefront BFS

In fact, wavefront finds paths from all sources to the goal.

Informed search

Sometimes you know:

• Accurate local edge lengths
• A possibly-inaccurate estimate of distances to goal

Informed search

I think blue is closer to the goal than green.

Informed search

The Manhattan distance is a heuristic for mazeworld.

Greedy search

• Code almost the same as for uniform cost search.
• Heuristic $h(n)$ instead of cost to node $g(n)$ as priority.

Discussion: greedy vs. UCS

1. Are there situations when greedy search finds a solution faster than uniform-cost search? If so, give an example. (What sort of maze, for mazeworld and a Manhattan-distance heuristic?)
2. Are there situations when uniform-cost search finds an answer faster than greedy search? Describe one.

Observations: Greedy search

• Does not typically give shortest paths.
• Fast or slow, depending on heuristic.
• Much memory or little, depending on heuristic.

A* search

A hybrid between greedy and uniform-cost search.

• UCS priority: $g(n)$, cost of getting to state $n$.
• Greedy priority, $h(n)$, heuristic from $n$ to goal.

A* priority: $f(n) = g(n) + h(n)$

Really? That works? Just add them?

A* search

$f(n)$ for the blue node is the best estimate of the cost of a path from start to goal through the blue node.

A* path optimality on a tree

A* search on a tree produces shortest paths if the heuristic is optimistic (also called admissible): it underestimates cost of path to goal from any node on the tree. (Multiple goals; finds closest.)

1. At any goal, $h(n) = 0$.
2. At any goal, $f(n) = g(n) + h(n) = g(n)$.

A* path optimality on a graph

A* search on a graph produces shortest paths if the heuristic is consistent (also called monotone).

consistent: For any vertices $N$, $P$, and goal $G$, the heuristic from N to G must be less than the cost of the edge from N to P plus the heuristic from P to G.

Discussion: greedy vs. A*

1. Are there situations when greedy search finds a solution faster than A* search? If so, give an example. (What sort of maze, for mazeworld and a Manhattan-distance heuristic?)
2. Are there situations when A* search finds an answer faster than greedy search? Describe one.
3. Are there situations where UCS finds an answer faster than A*? Describe one. (Hint: think about trees, and optimistic vs. non-optimistic heuristics.)

Nice discussion in thispaper.

Deriving heuristics

RELAX!

Discussion: deriving heuristics

Derive heuristics for each. Is each admissible? (Recall that we want consistent, not admissible, but proving a heuristic is consistent might take a few minutes.)

• Mazeworld
• Muli-robot mazeworld
• 8-puzzle

State space planning

Example from AIMA: vacuum world

State spaces

State transition diagram (many edges omitted)

Belief

Simplified vacuum world:

1. The robot is kidnapped (does not know start location).
2. The robot is blind (cannot detect location).
3. The robot has a compass (can take action reliably).

Find a sequence of actions to bring the robot home.

Belief

Reasoning:

• Either I'm home (square 0) or I'm not (square 1).
• If I'm in square 1, go West.
• If I'm in square 0, I still have to act, go West.

The sequence of actions W brings the robot home.

Belief

The sequence of actions WW brings the robot home.

Belief

What if the maze were bigger?

Does a plan even exist? Can we find one?

Belief states

Blue boxes: What I'm thinking about where I might be.

Blue boxes represent belief states.

Belief states

• Initial state: $\{0, 1, 2\}$
• West leads to state $\{1, 2\}$

Belief states

• Each location is in the set.
• Or it is not.

Discussion: belief states

1. If there are $n$ locations, at most how many belief states?
2. Can you find a plan for mazeworld/ blind robot in an infinitely long corridor?
3. What's a universal plan for a large empty square room of size 20x20?
4. What is a reasonable heuristic for blind robot? Write down a state and compute the heuristic. Is the heuristic optimistic?

Sequential planning

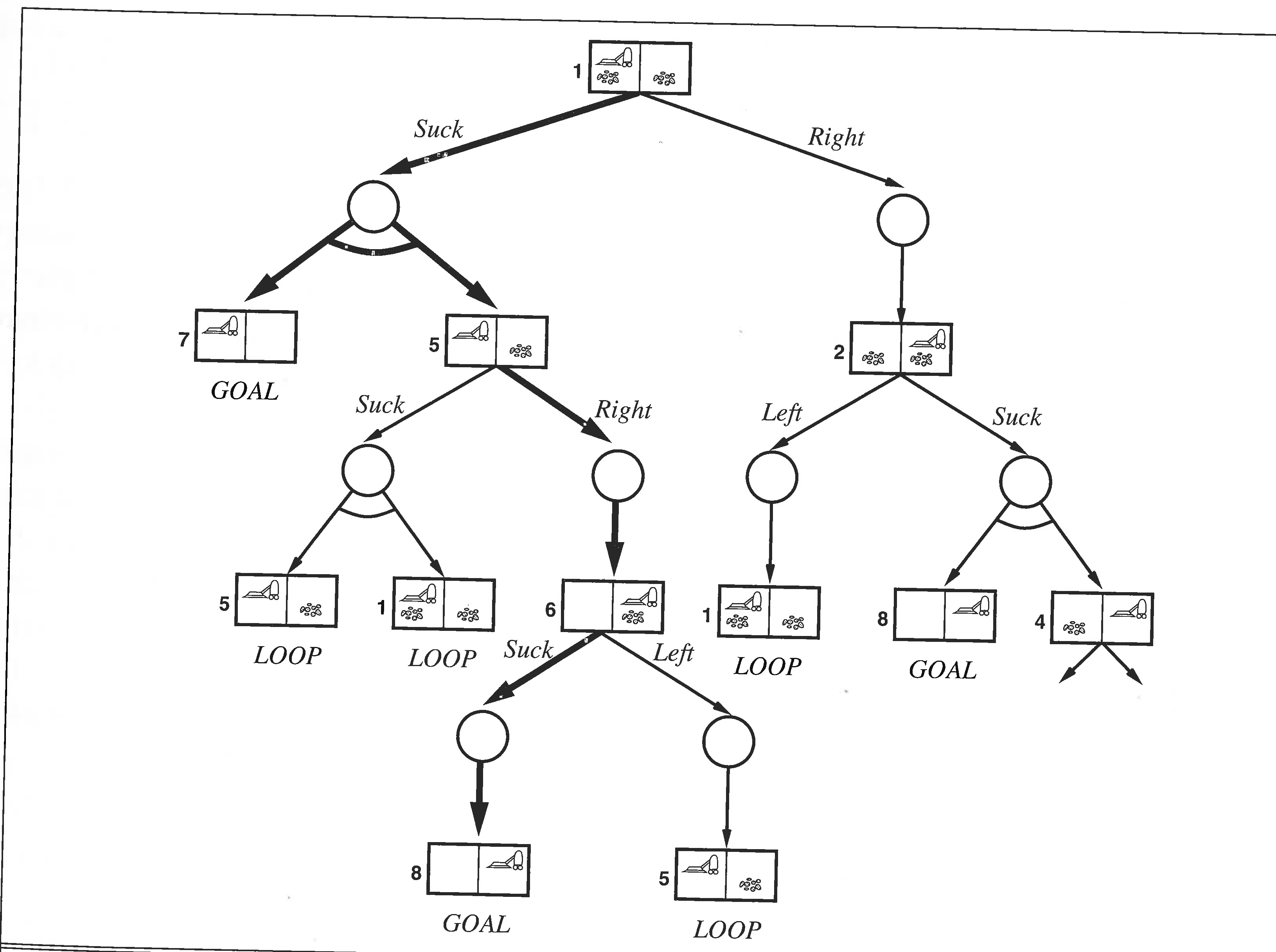
What if some actions are non-deterministic? Can we plan for a sequence of sensing and acting combinations? (Figure from AIMA.)