CS 76 / 176
Propositional logic
Professor Devin Balkcom
devin@cs.dartmouth.edu
office: Sudikoff 206
Notes
- Logic: AIMA, chapter 7
Logical agents
- So far, agents reason using belief states.
- Belief states explicitly represent set of possible worlds.
- Many possible worlds $\Rightarrow$ large belief space
We want compact representations of knowledge that allow agents to reason and draw conclusions.
sentence: our basic representation of knowledge; will restrict the space of possible worlds
Why logic?
- Richer representation of knowledge than belief space.
- Automated theorem proving.
- A good basis for probabilistic reasoning.
Knowledge base
knowledge base: set of sentences that describe things agent knows
tell $\rightarrow$ knowledge base $\rightarrow$ ask
tell: add sentence to knowlege base
ask: For every possible world for which all the sentences in the KB are true, is some other sentence true?
Example:
- tell: new sensor information at a time step
- ask: Given past sensor information, is there a wall?
Knowledge base
Viewed as constraints:
tell: adds a constraint on the belief space.
ask: if all constraints are satisfied, is the new constraint redundant (implied by what we already know)?
Inference
Both tell and ask may involve inference: combining old sentences to form new. Example:
- You have iocane powder.
- Iocane powder comes from Australia.
- Australia is entirely peopled with criminals.
Can we infer the new sentence, "You are a criminal?"
We need some precise rules.
Syntax
Syntax is a set of rules defining well-formed sentences.
This code is not well-formed under Java syntax:
System.print.outln[My name"]:This code is, under some other syntax:
++++++++[>++++[>++>+++
>+++>+<<<<-]>+>+>->>+[<]<-]
>>.>---.+++++++..+++.>>.<-.
<.+++.------.--------.>>+.>++.
Syntax gives the domain of possible sentences: the set from which sentences may be drawn.
Semantics
Semantics define the truth of the sentence w.r.t. each possible world, called a model.
Typically, sentences involve some variables, and variables have domains. A model is an assignment of values to variables.
Example. Is the sentence $x + y = 4$ true? (It satisfies the syntax for arithmetic expressions.)
- We could imagine $1 + 6 = 4$; just symbols.
- But we expect there to be some values of $x$ and $y$ (models) for which the sentence is true, and some other values for which it is not.
Semantics
We use semantics to define the set of worlds for which $x + y = 4$ is true:
| $x$ | $y$ | $x + y = 4$ |
| 0 | 0 | false |
| 1 | 0 | false |
| 3 | 1 | true |
| 1 | 3 | true |
| 2 | 2 | true |
Semantics
The table is incomplete. We need to know if sentence is true or false for each possible model, and there are infinitely many models.
- sentence $\rightarrow$
- model $\rightarrow$
Entailment
Let $\alpha$ and $\beta$ be sentences.
We say that $\alpha \models \beta$ iff for every model in which $\alpha$ is true, $\beta$ is true.
Example. In arithmetic, we say that $x = 0 \models x y = 0$. If you choose a model (say $x = 0$, $y = 6$) such that $x= 0$ is true, then the sentence $x y = 0$ is also true.
We let $M(\alpha)$ be the set of models for which a sentence $\alpha$ is true. Then $\alpha \models \beta$ means $M(\alpha) \subset M(\beta)$.
Entailment
Notice that the sentence $\alpha$ is the stronger (or at least no weaker) sentence, in that it constrains the space of possible models at least as much as $\beta$.
$\alpha \models \beta$
Entailment
If we have a set of sentences in the knowledge base, and we ask if these sentences entail some other sentence, are we creating a *new more powerful* assertion?
No. Any new sentence that is entailed is less constraining. But maybe in a more useful format.
Example. We have sentences "It is either sunny outside, or raining. If it is raining, no-one is skiing. It is raining."
Entailment
Any new sentence that is entailed is less constraining. But maybe in a more useful format.
Example. We have sentences "It is either sunny outside, or raining. If it is raining, no-one is skiing. It is raining."
The set of possible models of the world for which these sentences are true is smaller than the set of models for which no-one is skiing. (For example, it could be sunny, and no-one is skiing.) But we might still want to ask the knowledge base the question "is anyone skiing?"
Monotonicity
Monotonicity: Each new sentence added to the knowledge base further constrains the set of models that holds.
$\Rightarrow$ if we can prove that some sentence is entailed by a set of sentences in the knowledge base, then adding new sentences to the knowledge base will never invalidate that proof.
Propositional logic
Winter $\wedge$ NiceWeatherSunday $\Rightarrow$ Procrastinated
- Atomic sentence: a symbol that can take on the value true or false.
- Literal: atomic sentence, or negated atomic sentence
- Logical connectives: $\neg \vee \wedge \Rightarrow \Leftrightarrow$
Backus-Naur Form
Backus-Naur Form gives a recursive definition of syntax, the set of all legal sentences.
BNF, Prop. Logic
Sentence $\rightarrow$ AtomicSentence | ComplexSentence
AtomicSentence $\rightarrow$ True | False | Symbol
Symbol $\rightarrow$ P, Q, R, snowing, ...
ComplexSentence $\rightarrow$
$\neg$Sentence
| (Sentence $\wedge$ Sentence)
| (Sentence $\vee $ Sentence)
| (Sentence $\Rightarrow$ Sentence)
| (Sentence $\Leftrightarrow$ Sentence)
Model, Prop. logic
model: true false values for every atomic sentence
A world with the symbols isSnowing and isSunny would have the four models (true, true), (true, false), (false, true), and (false, false).
Review
- Model: assignment of values to variables
- Sentences: used to select a set of models ($winter$)
- Syntax: description of legal sentences
- Semantics: maps (sentence + model) to T/F
- Entailment: $\alpha \models \beta$. ("it is greater than 100 degrees" entails "it is greater than 32 degrees")
Entailment
Notice that the sentence $\alpha$ is the stronger (or at least no weaker) sentence, in that it constrains the space of possible models at least as much as $\beta$.
$\alpha \models \beta$
Propositional logic
Winter $\wedge$ NiceWeatherSunday $\Rightarrow$ Procrastinated
- Atomic sentence: a symbol that can take on the value true or false.
- Literal: atomic sentence, or negated atomic sentence
- Logical connectives: $\neg \vee \wedge \Rightarrow \Leftrightarrow$
PL Model
model: true / false values for every atomic sentence
A world with the symbols isSnowing and isSunny would have the four models
- (true, true)
- (true, false)
- (false, true)
- (false, false)
PL Semantics
Take a model and sentence and evaluate to T/F. Easy for atomic sentences. For complex sentences, write some rules using truth tables and apply recursively.
| $P$ | $Q$ | $P \wedge Q$ |
|---|---|---|
| false | false | false |
| false | true | false |
| true | false | false |
| true | true | true |
PL Semantics
Definition of the implies connective:
| $P$ | $Q$ | $P \Rightarrow Q$ |
|---|---|---|
| false | false | true |
| false | true | true |
| true | false | false |
| true | true | true |
$P \Rightarrow Q$ is true in models for which either $P$ is false, or both $P$ and $Q$ are true.
College life
Let's tell the knowledge base some sentences. Then ask if some other sentence is entailed.
- If I did not eat dinner, that implies that either the fridge was empty, or an assignment was due and I procrastinated. If the fridge was empty, or an assignment was due, and I procrastinated, then I did not eat dinner.
- If it is winter, and there was nice weather Sunday, I procrastinated.
- If the fridge is empty, my housemate will be mad.
Discussion: write these sentences using propositional logic.
College life
- $\neg$ Dinner $\Leftrightarrow$ FridgeEmpty $\vee$ (AssignmentDue $\wedge$ Procrastinated)
- Winter $\wedge$ NiceWeatherSunday $\Rightarrow$ Procrastinated
- FridgeEmpty $\Rightarrow$ HousemateMad
ask: if it is not winter, and I did not eat dinner, does that imply that my housemate is mad?
KnowledgeBase $\wedge \neg W \neg D \models H$?
Model checking
Method #1 for inference
- Seven symbols: D, F, P, A, W, H, N.
- Each symbol can take the value true or false.
- Consider all $2^7$ assignments of true/false values.
If $H$ is true for all models in which all sentences in (KB and $\neg W \neg D$) are true, then $H$ is entailed by $W \neg D$.
Inference rules
Method #2 for inference
- Apply some inference rules to the knowledge base (together with $\neg W \neg D$) to construct new sentences.
- Show that the sentence $H$ is entailed
We haven't seen inference rules yet. Can be effective, but it may be difficult to find inference rules that allow the construction of the particular sentence.
Contradiction
Method #3 for inference
- Add $\neg W \neg D$ and $\neg H$ to the knowledge base
- Show that this induces a contradiction: there exists a sentence that is entailed, and the negation of that sentence is also entailed.
Example: Show that are no models for which $\neg W \neg D$ holds, but $H$ does not.
Always works in principle for PL, but computationally expensive and the proof is not constructive.
Conjunctive Normal Form
Simplify into a standard form.
$A \Rightarrow B$ becomes $\neg A \vee B$.
(Easy to prove — just look at truth tables!)
CNF rules
- Eliminate $\Leftrightarrow$, replace with $(\alpha \Rightarrow \beta) \wedge (\beta \Rightarrow \alpha)$.
- Eliminate $\Rightarrow$, replace with $\neg \alpha \vee \beta$
- Move $\neg$ inwards:
- $\neg(\neg \alpha) : \alpha$
- $\neg(\alpha \wedge \beta): \neg \alpha \vee \neg \beta$ (DeMorgan)
- $\neg(\alpha \vee \beta): \neg \alpha \wedge \neg \beta$ (DeMorgan)
- Distribute $\vee$ over $\wedge$:
- $\alpha \vee (\beta \wedge \gamma) \rightarrow (\alpha \vee \beta) \wedge (\alpha \vee \gamma)$
Now we have a conjunction of disjunctions of literals:
$(A \vee \neg B \vee C) \wedge$
$(C \vee \neg D) \wedge \ldots$
Logical equivalence
CNF conversion relies on logical equivalences.
For example, commutativity tells us that for all models and sentences,
$(\alpha \wedge \beta) \models (\beta \wedge \alpha)$
We write:
$(\alpha \wedge \beta) \equiv (\beta \wedge \alpha)$
"Commutativity tells us?"
Don't let me get away with that. How do we prove it?
CNF example
College life:
- $\neg D \Leftrightarrow F \vee (A \wedge P)$
- $W \wedge N \Rightarrow P$
- $F \Rightarrow H$
CNF example
Eliminate double implications:
- $\neg D \Leftrightarrow F \vee (A \wedge P)$
- $W \wedge N \Rightarrow P$
- $F \Rightarrow H$
CNF example
Eliminate double implications:
- $\neg D \Leftrightarrow F \vee (A \wedge P)$
- $\neg D \Rightarrow F \vee (A \wedge P)$
- $F \vee (A \wedge P) \Rightarrow \neg D$
- $W \wedge N \Rightarrow P$
- $F \Rightarrow H$
CNF example
Replace implications with $\neg \alpha \vee \beta$:
- $\neg D \Rightarrow F \vee (A \wedge P)$
- $\neg (\neg D) \vee (F \vee (A \wedge P))$
- $F \vee (A \wedge P) \Rightarrow \neg D$
- $\neg (F \vee (A \wedge P)) \vee \neg D$
- $W \wedge N \Rightarrow P$
- $\neg (W \wedge N) \vee P$
- $F \Rightarrow H$
- $\neg F \vee H$
CNF example
Move $\neg$ inwards:
- $\neg (\neg D) \vee (F \vee (A \wedge P))$
- $D \vee (F \vee (A \wedge P))$
- $\neg (F \vee (A \wedge P)) \vee \neg D$
- $(\neg F \wedge \neg (A \wedge P)) \vee \neg D$
- $(\neg F \wedge (\neg A \vee \neg P)) \vee \neg D$
- $\neg (W \wedge N) \vee P$
- $\neg W \vee \neg N \vee P$
- $\neg F \vee H$
CNF example
Distribute $\vee$ over $\wedge$:
- $D \vee (F \vee (A \wedge P))$
- $(\neg F \wedge (\neg A \vee \neg P)) \vee \neg D$
- $\neg W \vee \neg N \vee P$
- $\neg F \vee H$
After:
- $D \vee ((F \vee A) \wedge (F \vee P))$
- $(D \vee F \vee A) \wedge ( D \vee F \vee P))$
- $\ldots$
CNF example
It's in CNF! A conjuction of disjunctions!
- $(D \vee F \vee A) \wedge ( D \vee F \vee P))$
- $(\neg F \vee \neg D) \wedge (\neg A \vee \neg P \vee \neg D))$
- $\neg W \vee \neg N \vee P$
- $\neg F \vee H$
CNF example
Sanity check. Is
$\neg D \Leftrightarrow F \vee (A \wedge P)$ $\equiv$
$(D \vee F \vee A) \wedge ( D \vee F \vee P))$ ?
Let's assume $\neg D$. Then $F \vee (A \wedge P)$ is true, from the double implication. Now looking at the CNF form:
$(False \vee F \vee A) \wedge ( False \vee F \vee P))$
$(F \vee A) \wedge (F \vee P))$
So either F is true, or both A and P are true, which is the same result we got from the original form. Sane.
Validity and satisfiability
A valid sentence is true for all models: $A \vee \neg A$
A satisfiable sentence is true for some models: $A$
$A \wedge \neg A$ is not satisfiable.
Sentence $\alpha$ is valid iff $\neg \alpha$ is unsatisfiable.
Satisfiability of a propositional logic sentence was one of the first problems shown to be NP-complete. We have seen an exponential algorithm already: model-checking.
The deduction theorem
For any sentences $\alpha, \beta$,
$\alpha \models \beta$ iff $(\alpha \Rightarrow \beta)$ is valid.
So what?
- Entailment is a concept, and involves two sentences.
- $\alpha \Rightarrow \beta$ is a single sentence in PL.
How do we prove that $\alpha \Rightarrow \beta$ is valid?
Model checking? What would happen if we added hundreds of symbols, none of which appear in the KB or in $\alpha$ or $\beta$? Model checking would look silly.
Proof by contradiction
Goal: prove that $\alpha \Rightarrow \beta$ is valid.
Maybe easy to prove a sentence unsatisfiable:
$A \wedge \neg A$ is unsatisfiable, even if we add new sentences, due to monotonicity.
So prove $\neg (\alpha \Rightarrow \beta)$ is unsatisfiable. In CNF:
- $\neg (\neg \alpha \vee \beta)$ unsatisfiable
- $\alpha \wedge \neg \beta$ unsatisfiable
So, add $\neg \beta$ to KB and show there are no models for which this is true. (Proof by contradiction.)
Reasoning patterns
Inference rule example. Prove unsatisfiable:
- $\alpha \Rightarrow \beta$
- $\alpha \Rightarrow \neg \beta$
- $\alpha$
Model checking hard, if many symbols.
But perhaps we could combine sentences, forming 'weaker' sentences (true for at least as many models.) If new sentences unsatisfiable, so were the original.
Modus ponens
Unsatisfiable?
- $\alpha \Rightarrow \beta$
- $\alpha \Rightarrow \neg \beta$
- $\alpha$
modus ponens:
$\frac{\alpha \Rightarrow \beta, \alpha}{\beta}$
- Sentences (1) and (3) imply $\beta$ by modus ponens.
- Sentences (2) and (3) imply $\neg \beta$ by modus ponens.
- $\beta \wedge \neg \beta$ is unsatisfiable, Q.E.D.
And-elimination
Another convenient reasoning pattern is and-elimination:
$\frac{\alpha \wedge \beta}{\alpha}$
Proof by inference
A proof proceeds using a sequence of applications of inference rules. What do we do in AI? We search.
Resolution
How many inference rules do we need?
Only resolution. (One inference rule to rule them all...)
Simple case, unit resolution:
$\frac{l_1 \vee l_2 ... \vee l_k, \neg l_i}{l_1... l_{i-1} \vee l_{i+1} \vee ... l_k}$
One of the first literals must be true, and we know which one it's not. So it must be one of the others.
Resolution
The complete resolution rule:
$\frac{l_1 \vee l_2 ... \vee l_k, \hspace{10pt} m_1 \vee \ldots m_n}{l_1... l_{i-1} \vee l_{i+1} \vee ... l_k \vee m_1... m_{j-1} \vee m_{j+1} \vee ... m_n}$,
where $l_i$ and $m_j$ are complementary literals.
Delete complementary literals from a pair of disjuctions, and combine the remaining symobls into a single disjunction.
Resolution
$\frac{l_1 \vee l_2 ... \vee l_k, \hspace{10pt} m_1 \vee \ldots m_n}{l_1... l_{i-1} \vee l_{i+1} \vee ... l_k \vee m_1... m_{j-1} \vee m_{j+1} \vee ... m_n}$,
where $l_i$ and $m_j$ are complementary literals.
Does it make sense? Consider this case:
$(A \vee B \vee C \vee D) \wedge (\neg A \vee E \vee F)$.
- $A$ true: we can see from $\neg A \vee E \vee F)$ that either $E$ is true or $F$ is true.
- $A$ false: at least one of $B$, $C$, or $D$ must be true.
Add $B \vee C \vee D \vee E \vee F$ to KB.
Things to prove:
- Entailment. Assume sentence $\alpha$ is true. Does this guarantee that $\beta$ is true?
- Satisfiability Do there exist any models under which sentence $\alpha$ is true?
Minesweeper entailment example:
0.. 1x. 0..
Prove that there is be a mine at x, in all models.
But for Sudoku, it might be sufficient to show that there is one assignment of values to locations, before publishing the puzzle: satisfiability.
Wumpus world
Example: No pit in starting location, (1, 1)
$\neg P_{1,1}$
Wumpus world
Another rule is that if there is a pit in a square, then there is a breeze in any square adjacent to the pit. For example,
$P_{3,1} \Rightarrow B_{4_1} \wedge B_{3_2} \wedge B_{2_1}$
Furthermore, if there is *not* a breeze in a square, then there is not a pit in any adjacent square.
$\neg B_{2, 2} \Rightarrow \neg (P_{2,1} \vee P_{3, 2} \vee P_{2,3} \vee P_{1, 2})$
There are a lot of rules like this.
Wumpus world
There are a lot of rules like this. We didn't say there was a pit in 3, 1, for example. We said if there is a pit in 3, 1, then there is a breeze in the three adjacent squares.
So we need a set of rules for every precept, in every square. Even in this relatively small 4x4 Wumpus game, there are many symbols and many rules in the knowledge base.
Over time, agent takes actions, gets new information from precepts, and would like to prove things logically before taking the next action. (For example, that there is no pit in the next square, under any model. Entailment.)
Wumpus world
Rules: No pit in the starting square, and a square is breezy if and only if there is a breeze in the neighboring square:
- $R_1: \neg P_{1, 1}$
- $R_2: B_{1, 1} \Leftrightarrow P_{1, 2} \vee P_{2, 1}$
- $R_3: B_{2, 1} \Leftrightarrow P_{1, 1} \vee P_{2, 2} \vee P_{3, 1}$
Breeze percepts for the first two squares:
- $R_4: \neg B_{1, 1}$
- $R_5: \neg B_{2, 1}$
We would like to show that the sentence $\neg P_{1, 2}$ is entailed by the KB.
Resolution search
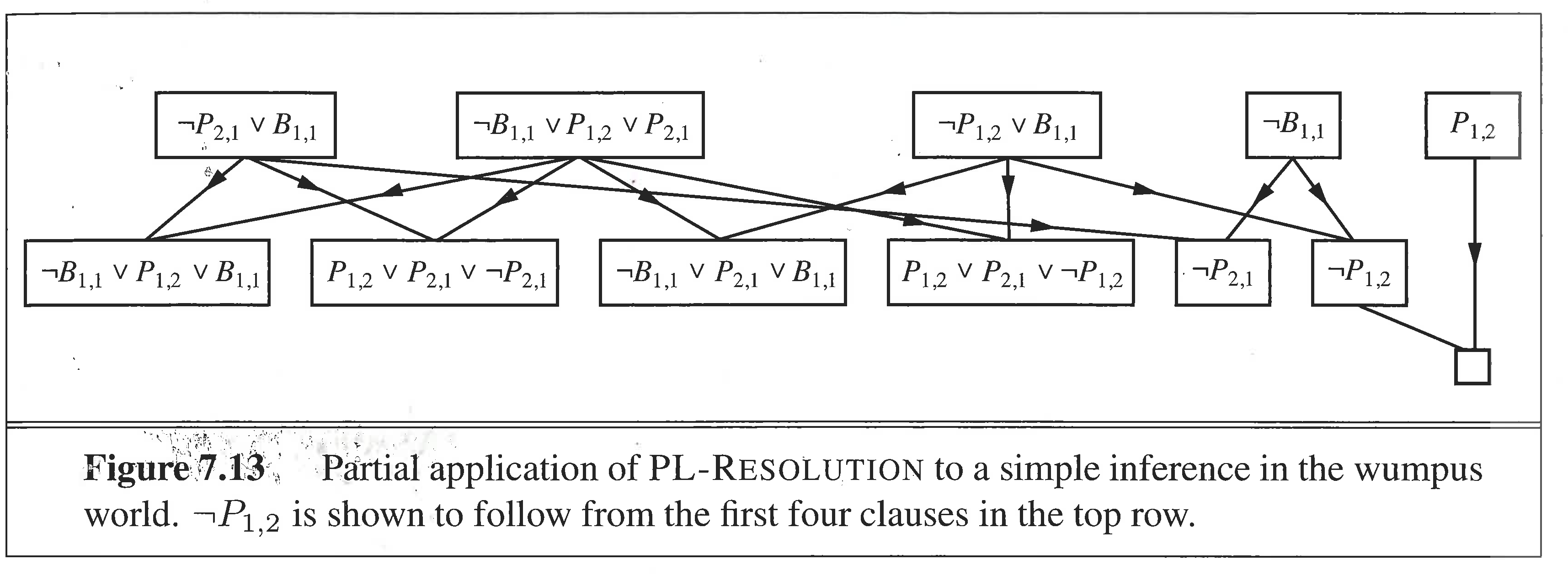
Completeness of resolution
Resolution closure of a set of clauses is the set of all clauses that can be found by repeated application.
Resolution closure is finite because there are finitely many symbols, and resolution always creates a new clause without repeated symbols.
Ground resolution theorem: If a set of clauses is unsatisfiable, then the resolution closure of those clauses contains the empty clause. Proof by showing that if the resolution closure does not contain empty clause, then S satisfiable, page 255.
Completeness of resolution
Resolution constructs the counter-example when it terminates.
Horn clauses
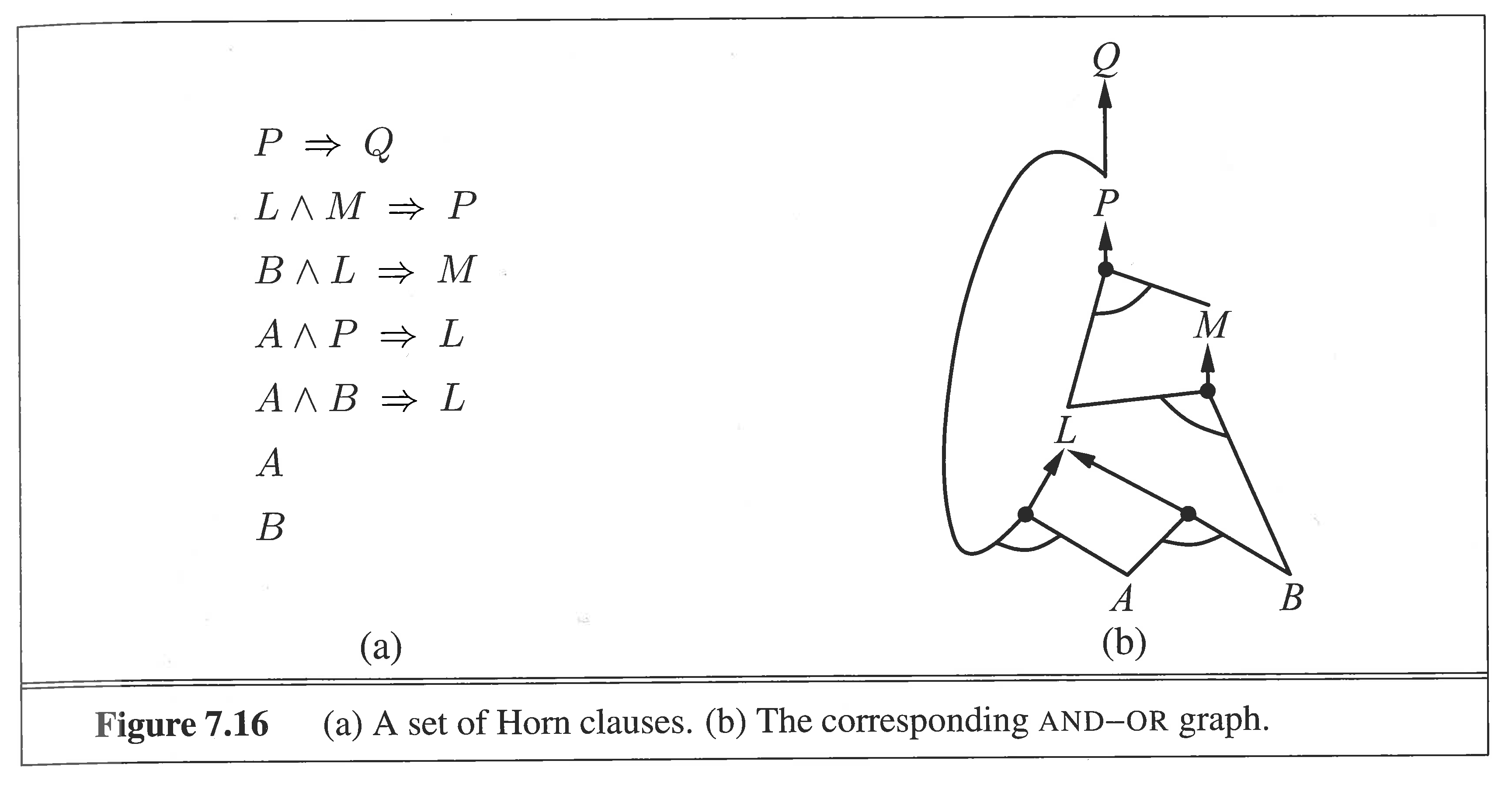
Can be used to prove entailment of a symbol in linear time.
SAT problems
Fromulation of Sudoku as a SAT problem.
Note: a complete SAT solver that runs in bounded time can be used to prove entailment, since entailment can be proven by showing unsatisfiability of $\alpha \wedge \neg \beta$.
- DPLL: A complete backtracking model-enumeration approach. Because this algorithm is complete, it could be used to prove entailment.
- WALKSAT. A random-walk model-checking approach. Because the random walk could take an infinite time to explore all models, can't prove unsatisfiability. Can be fast if satisfiable, and trivial implementation.
DPLL
Examples based on DPLL: CHAFF, minisat, and SAT4J.
Interestingly, SAT4J is integrated into Eclipse, and used to check dependencies of Eclipse modules.
Enumeration of models, with a few improvements:
- Early termination. If any literal evaluates to true, clause does. If every literal false, clause false, prune subtree.
- Pure symbols. A symbol that is only positive or negative in a clause. If there is any model satisfying the sentence(s), then there is one in which the pure symbol is set to true.
WALKSAT
Pick a random model (assignment). If it satisfies the sentences, we're done. Otherwise, randomly pick a symbol to swap between true and false. With some probability, we either pick a symbol that satisfies the most new clauses, or pick some other symbol.