Representing displacements
Displacements are combinations of rotations and translations, pure rotations, or pure translations. We would like to represent displacements mathematically, so that we can build algorithms that generate or interpret rigid body motions.
There are three things we want to do:
- Represent (describe) displacements
- Transform a rigid body system using a displacement
- Given a point in one coordinate system, find its coordinates relative to a different frame
How we do each depends somewhat on how we represent rigid bodies. For now, assume the rigid body system is described as a collection of points in the plane or in space, with a 2-vector or 3-vector giving the Cartesian location of each point relative to some frame.
Translation is easy to represent: We just use a vector describing the magnitude of the components of the translation along the axes of some frame.
Transformation by a translation is then implemented by vector addition of each point in the system and the translation vector. The inverse of a translation is represented by the vector multiplied by negative one.
Rotation matrices
Rotations leave one point fixed. Since any displacement can be viewed as a rotation about some arbitrary point, combined with a translation, it follows that a rotation can be viewed as a translation, a rotation about the origin, and a translation that is the inverse of the first translation. For this reason, we will only consider rotations about the origin.
Two dimensions
Consider a rotation in two dimensions about the origin by the angle \(\theta\). We could represent this rotation just by a single number, the value of \(\theta\).
How can we then implement transformation by rotation? Probably you’ve seen a formula that looks like this:
\(x' = Rx\)
where
\(R = \left[ \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right].\)
Why should this be the right formula? Let’s try a few points. First, take the point $x^T = (1, 0) $. We multiply through and get \(x'^T = (\cos \theta, \sin \theta)\), which is geometrically what we expect. Then, take the point $x^T = (0, 1) $. Multiplication gives you \(x'^T = (-\sin \theta, \cos \theta)\), also what we expect.
This is for me the easiest way to remember the correct elements in a rotation matrix – otherwise I get very confused about which signs, sines, and cosines go where.
This interpretation of the rotation matrix (the columns are the coordinates of the transformed world frame) also lets us see a few important properties of rotation matrices:
- The columns are of unit length (take the dot product of a column with itself. It’s one.)
- The columns are orthogonal (take the dot product of two columns. It’s zero.)
- The determinant is 1.
There is a geometric interpretation of the determinant of a matrix – it describes how much the matrix “stretches” points away from each other. We won’t go into the details, but a rotation preserves areas and volumes of rigid bodies (not surprising!), and thus has determinant one. There is another type of matrix that has orthogonal columns of unit length but determinant -1 – these are called reflections.
The set of all possible 2D rotation matrices has a name: the “special orthogonal group 2”, abbreviated SO(2). The “special” means determinant 1 (not -1), and the orthogonal means the columns are orthogonal. You just have to remember that these matrices also have columns of unit length.
I claim that if properties 1, 2, and 3 above hold, then the matrix represents a rotation. Specifically, for any two points x and y,
- One point is left fixed (the origin)
- ||Rx - Ry|| = ||x - y|| (it’s a displacement)
- (We should also prove that it is not a reflection, but we will skip this part.)
Result a) is easy to show. Multiply R by a vector of zeros. You get a vector of zeros.
To prove b), we need to prove an auxilliary fact first. Orthogonal matrices have an interesting property: their transpose and their inverse are the same. \(R^T R = I\). So to invert a rotation, just transpose the matrix! I demonstrated this in class, and it’s quite easy to show. Multiply rows of \(R^T\) by columns of \(R\); this is equivalent to taking dot products of two columns of \(R\), since rows of \(R^T\) are formed from columns of \(R\). If same row, column, then the result is \(1\), since the columns of \(R\) have unit length. If not same row, column, then result is \(0\), by orthogonality of columns of \(R\). So there are \(1\)s along the diagonal of the result, and \(0\)s elsewhere; an identity matrix.
Now let’s prove that \(||Rx - Ry|| = ||x - y||\). We’ll work backwards from the result. For a formal proof, reverse the steps.
First, square both sides
\(||Rx - Ry || ^2 = (Rx - Ry)^T (Rx - Ry)\)
\((Rx - Ry) ^T = (Rx)^T - (Ry)^T\)
$ = x^T R^T - y^T R^T$
So we have
\((x^T R^T - y^T R^T) (Rx - Ry)\)
\(x^T x - x^T y - y^T x + y^T\)
Same as right hand side, expanded.
The space of nxn matrices satisfying these properties is called the special orthogonal group, SO(n). SO(2) is the space of rotation matrices that rotates points in R^2.
How many degrees of freedom does SO(2) have?
- 4 numbers
- Some length constraints
- Some dot product constraints.
\(4 - 3 = 1\)
In fact, we can parameterize this by \(\theta\).
How many DOF does SO(3) have? Count constraints. We get 9 - 3 - 3 = 6. In class, we also derived the number of degrees of freedom for SO(4).
Three dimensions
Who cares about special orthogonal matrices? Why not just use the angle \(\theta\) to represent rotations? In 2D, that’s perfectly fine, but in 3D, which \(\theta\) do you use?
Euler angles
You could pick three angles, describing, for example, the rotation about the X axis by angle \(\alpha\), followed by a rotation about the Z axis by angle \(\beta\), followed by a new rotation about the X axis by angle \(\gamma\), as shown on this Wikipedia page.
This representation is called a “XZX” Euler angle representation. It’s ok in some cases, but imagine a simple rotation about the X axis by \(\theta\). The rotation about the Z axis is zero. There are an infinite number of choices of combinations for \(\alpha\) and \(\gamma\) – they just have to sum to \(\theta\)!
This can be problematic. For example, if you just sample the three angles uniformly, you might hope to get a “uniform” distribution of rotations. What does a uniform distribution of rotations mean? I’m not sure, but this isn’t it – a lot of the rotations you get will tend to be rotations about, or nearly about, the X axis.
The choice of XZX axes was arbitrary. There are also ZYZ axes, XYZ angles, and other conventions.
SO(3) rotation matrics
Some things are simplified if we use a matrix (with nine numbers) instead of the three Euler angles to describe rotations. The columns of the matrix represent the location of each of the axis of the base frame after the rotation, so the geometric interpretation seems to me to be much much simpler than for Euler angles. There are constraints on these nine numbers: the columns are orthogonal, of unit length, and the determinant is one.
The name for the space of rotation matrices is SO(3): the special orthogonal group 3. If we remember the interpretation of columns as transformations of the vectors along the axes of the base frame, it’s easy to write down several special cases of rotation matrices. For example, \(R_z(\theta)\) is the rotation matrix describing rotation around the z axis by the angle \(\theta\), and the columns are similar to those for the 2D rotation matrix. (2D rotations are always around the z-axis.)
\(R_z(\theta) = \left[ \begin{array}{ccc} \cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \\ \end{array}. \right]\)
There’s also a convention that we need to keep track of. Given an axis, do we rotate around it clockwise or counterclockwise? We will use right-handed rotation matrices. Point your right thumb along the axis you want to rotate around; your fingers curl in the positive direction.
Homogeneous coordinates
Every displacement is a composition of a rotation about any point you choose, and a translation. Let’s say that you use a rotation matrix R to represent rotations, and a vector v to represent translations. Then a displacement transformation can be implemented with:
\(p' = Rp + v\)
The inverse is given by
\(p = R^{-1}(p' - v) = R^{T}(p' - v).\)
There’s nothing wrong with that, but it would be nice to represent a displacement by just a matrix, and implement the transformation by a simple multiplication. There’s a trick to this. We represent the points in the rigid body using four numbers, p = (x, y, z, w). For now, let w = 1. Then we can write a 4x4 displacement matrix that looks like:
\(T = \left[ \begin{array}{cccc} R & & & v \\ 0 & 0 & 0 & 1 \end{array} \right]\).
This is called a homogeneous coordinate system. For displacements, w is always 1, but it can take on other values. The physical location of p is interpreted as \((x/w, y/w, z/w)\). Why do we care? Well, if you set \(w = 0\), then you can describe a point at infinity, in a particular direction. Why would you want to? Well, a translation can be viewed as a translation about a point at infinity.
Homogeneous coordinates also show up in computer graphics, and are useful in studying the geometry of projections (since you can scale along a vector by just changing the parameter w.) For now we will not worry too much about projective geometry, but we will use homogeneous transform matrices to represent displacements.
Other ways to represent rotations: Axis-angle, Quaternions
You could describe a rotation by three numbers that describe a rotation axis, together with an angle by which to rotate. A variation of this is to use the length of the rotation axis vector to give the magnitude of the rotation.
Quaternions are another way of representing rotations using four numbers. They have some nice properties, particularly in terms of uniform sampling and stability of numerical computations, and are used very widely for implementations of robotics and graphics algorithms. I’d recommend you read up on them on your own.
Converting between rotation representations
Sometimes it’s necessary to convert between rotation representations. Rodrigues formula lets you convert from axis-angle to rotation matrix. It’s easy to convert from an Euler-angle representation to a rotation matrix – just write three matrices down representing each coordinate axis rotation, and multiply.
Kinematics with homogeneous coordinates
A homogenous transform matrix has the following structure:
\(T = \left[ \begin{array}{cccc} R & & & v \\ 0 & 0 & 0 & 1 \end{array} \right]\).
We can use a homogenous tranform matrices three ways:
- The matrix represents (describes) a displacement. (Matrix as a data structure.)
- The matrix can premultiplied by a point \(p\) to find out where the point would end up after applying the represented displacement. \(p' = T p\). (Matrix-vector multiplication.)
- The matrix can be used to transform between coordinate systems. (Matrix-matrix multiplication.)
Here is a figure of situations 1 and 2:
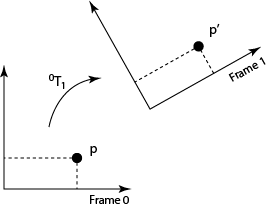
In situation 1 and two, both \(p\) and \(p'\) have coordinates expressed relative to frame 0. They are 3-vectors – homogenous points with the third element 1.
and here is a figure of situation 3.
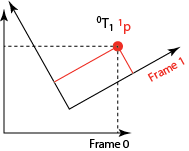
In this figure, \(p^1 = (^1x, ^1y, 1)\) is a point expressed in homogeneous coordinates relative to the frame 1: \(^1x\) is the scalar length of a vector in the direction of frame 1’s first axis, starting at the origin of frame 1.
In order to change coordinates to find \(^0p\), we imagine a point \(p\) in frame 0, such that applying the displacement would displace that point \(p\) to a location \(p'\) that is the same location as \(^1p\). So the vectors have the same elements: \(p = ^1p\). Since \(^0T_1 p = p'\), it follows that \(^0T_1 ^1p = ^0p\).
We can also chain results. Imagine we have a point \(^3p\), expressed in coordinates relative to a frame 3. If we have transform matrices \(^0T_1\), \(^1T_2\), \(^2T_3\), then we can express the point \(p\) relative to any frame we want. For example, \(^2p = ^2T_3 ^3 p\). Once we have \(^2p\), premultiply by \(1^T_2\) to get \(^1p\). So to compute \(^0p\),
\(^0T_1 ^1T_2 ( ^2T_3 ^3p ) = ^0p\).
In fact, since matrix multiplication is associative, we can see that
\(^0T_3 = {^0T_1} {^1T_2} {^2T_3}\).
Notatice that notationally, we can remember that subscripts and superscripts “cancel” during matrix multiplication.
In fact, we can also see that transform matrices can be used to change the frame with respect to which a transform is described. Each column of the transform matrix essentially describes a point. The first columns describe points a unit distance from the origin, rotated by some amount around the origin. The last column describes a point relative to the same frame of reference.
We attached frames to the joints of a planar serial robot arm, and wrote simple transform matrices expressing the relationship between adjacent frames.
At this point you should see that homogenous tranforms have some nice properties. We don’t need separate cases for rotation and translation, and in fact, there is a one-to-one correspondance between transform matrices and displacements. Multiplication of two transformation matrices yeilds another tranformation matrix: we say that the space of homogeneous transform matrices forms a group. Displacements also form a group. So we can compose a sequence of displacements by simple matrix multiplication, finding the net effect of the displacement. Indeed, forward kinematics of serial arms is exactly this: finding the net effect (a displacement) of applying rotations or translations at each joint.
Denavit-Hartenberg parameters for serial robot arms
The wikipedia page on Denavit-Hartenberg parameters is quite good, and includes an animated movies showing the geometry.