In the this lecture we will discuss the detailed design of the crawler’s data structures. We discuss double linked lists and hash tables for speeding up the search for unique URLs. The major data structures include the hash table, a double linked list for holding DNODEs (general dictionary elements). DNODEs maintain spointers to a URL structure called URLNODE which in turn maintain state information associated with the webpage crawled such as its depth as well as control information for the algorithm such as the visited variable indicating if the webpage as been crawled already or not.
The complexity of the design is the crawler is mostly carried by the data structure design making the code relatively non complex. Putting effort into the design of smart data structures saves a significant amount of coding. Poor data structure choice leads to complex and complicated code.
We plan to learn the following from today’s lecture:
There are a number of important data structures used to implement the crawler. In fact these data structures are also used to implement the indexer which will be the subject of Lab5. In what follows, we discuss each of the structures.
A key problem is the design of the data structure representing the information that must be maintained for each URL. This includes the URL name itself and the depth associated with the URL (e.g., 0, 1, 2, etc.) and a control flag used by the crawler program to mark if the URL has been visited or not. Visited indicates that the webpage has been downloaded by the wget command and the URLs extracted from the page and inserted into the double linked list maintained by the DICTIONARY structure.
A possible implementation of the URL element is the following URLNODE:
First some general comments. We need a structure that could be used to first define if a URL is unique. If it is unique we want to store it and then at a point later (after we have process one or more URLs) we want to download the webpage associated with this stored URL and then extract and store unique URLs embedded in that page. A obvious structure is some list (single or double linked list) that is a list of URLNODES that can be searched and items added. However, the access to this data structure is linear. If we are unlucky, we need to parse all the data structure in order to retrieve the URL.
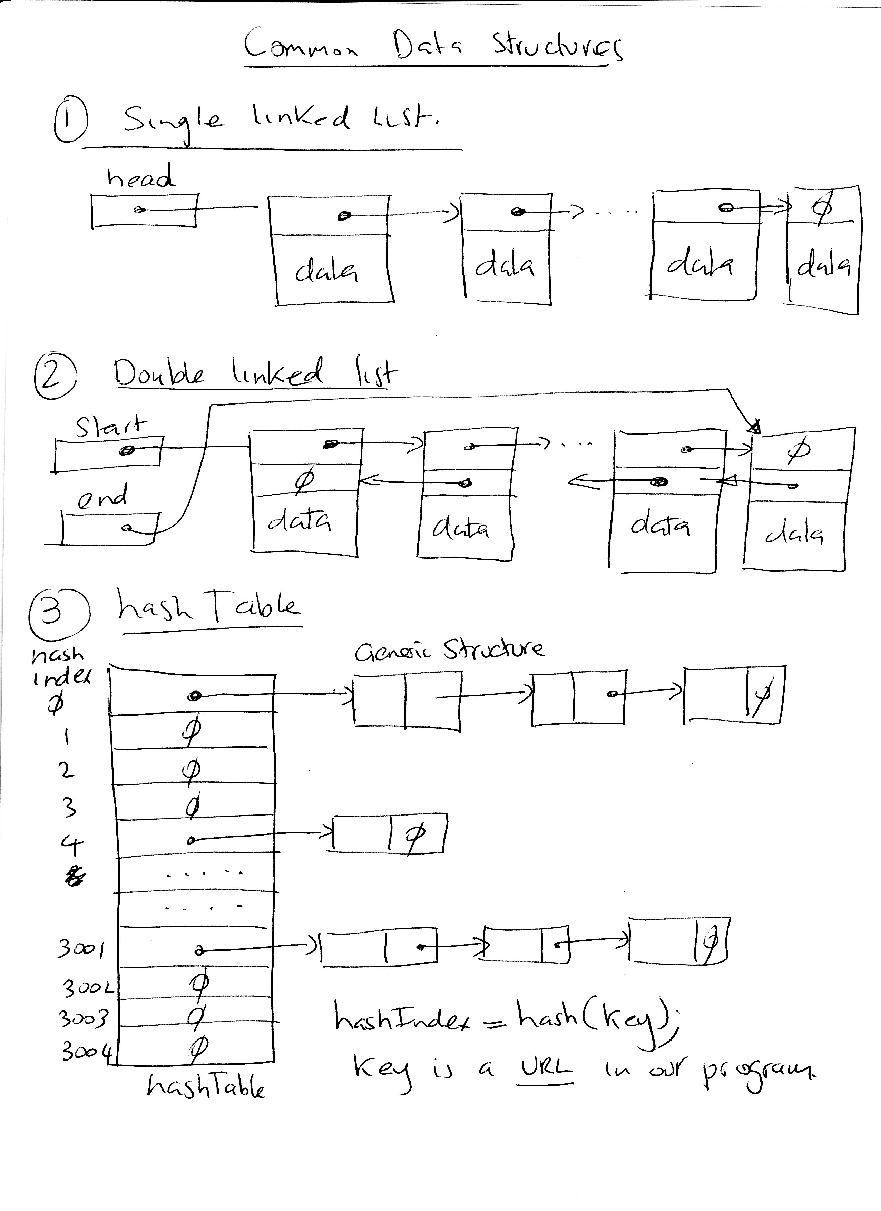
From below we define a double linked list (start and end) of DNODES. The DNODE holds a void pointer (data) to a URLNODE (which holds the URL name, depth and visited elements). It also holds forward and reserve pointers to a double linked list of DNODE structure instances which hold information related to other URL that the program deems unique. The assume being that if there is a DNODE/URLNODE pair on the list (start, end) then it unique.
Link lists are fundamental data structures that you will see time and time again. They are used for many applications from queuing process control blocks in the Linux kernel scheduler to handling application requests at a webserver. Linked lists like DNODE *start, *end consist of a number of elements (i.e., DNODES) grouped or linked together in some order (could be unordered or ordered based on some requirement - alphabetically, numerically, priority to name a few criteria). Link lists are designed to make insertion and removal of elements very efficient. For example, DNODE is a double linked structure with forward and backward pointers making insert very efficient at any point in the list of elements.
Importantly, we make use of dynamic allocated memory using malloc at runtime to create both URLNODE/DNODE pairs when we need them. This makes good design sense because we don’t know if crawler will come across 50 or 5000 URLs, right. Therefore we can’t (and never should) hard code a hack to do this. Better to design an intelligent program that grows as needed in a scalable manner. We do this in our design and implementation.
There are a number of different link lists:
Single link lists, where a single pointer allows the program to traverse the list from start to finish. End of
the list is denoted as a NULL pointer
Double link lists, where elements are linked with two pointers rather than one and the list can be
traversed in both forward and backward directions. In the case of our structure *start points the
first DNODE linked and *end to the last one. Therefore traversing can be either direction. It
is easy to insert at the start and end. It is also very easy to insert at any point in the list
since DNODEs maintain forward and backward pointers to neighboring DNODEs. End of
the list is denoted by a NULL pointer. Empty list is denoted by start and end being NULL
pointers.
Circular link lists, where the last element is linked to the first element instead of being NULL.
Note, we hold off on a discussion of the key element until below.
The performance of such a structure is O(n). Because we may have hundreds of URLNODES linked to this list at anyone time we want to design a faster access structure - e.g., O(1). For example, if you crawl the www.cs.dartmouth.edu to a depth of 2 there will be approximately 200 unique. The pure list solution would make the operation of the crawler slow. So how can we speed up this operation. We need a smart data structures.
One possible implementation can be based on a dictionary, i.e., a generalized hash table (like that we have seen in the assignment about the design of the index).
Each element of the dictionary is defined as follows:
Clearly, if we are dealing with small numbers of URLs then a linked list if the right cup of tea. But we are not. Performance O(n) would not be a good design for 10,0000 URLs. You have time for the tea to grow in Darjeeling before the crawl completed. Order(1) would be nice!
The use of a hash table would speed our execution significantly. Hash tables and functions support one of the most effective types of searches: hashing. A hash table consists of an array of some length where data is accessed via a special index called (in a general sense) a key. The ideas behind the hash table is to create a mapping between the key (in our application the key is the URL e.g., www.cs.dartmouth.edu/˜nlane) and the index into the hash table array - the index is called has value. Keys can almost be anything - URL, time of day, IP address (routers use hash tables to look up the next hop to forward an IP packet), name - but hash values are always an integer that identifies the slot of the hash table array.
The great innovation in hash tables is that computing the index (a hash function does that - the one we use is called hash1(char *)) is done in constant time! Therefore no matter how many URLs (elements) we have we will always search (to determine the uniqueness of the URL before we inset it in the list) in constant time. That is a very nice scaling property of the design. In ideal cases (i.e., unrealistic) a function will guarantee that no two keys will hash to the same slot (i.e., have the same hash value). However, in reality this is not the case. Different keys may with small probability (assuming that the size of the table in relation to the maximum number of elements is reasonable but clearly we assume that the number of entries in the table is small in comparison to the potentially large number of URLs encountered) have the same hash index. As a consequence most hash functions will map two or more keys to the same slot in the table. This is called collision. And a good hash function will be designed to limit collision in an attempt to randomly distribute DNODEs/URLNODEs elements across the table.
Here is how the process works.
Given the following:
- a key www.cs.dartmouth.edu/ campbell
- a hash function hash1()
- a hash table DNODE *hash[MAX_HASH_SLOT] of a certain size (here we choose a large value of
MAX_HASH_SLOT = of 10000)
Then we can do the following:
hashIndex = hash1(‘‘www.cs.dartmouth.edu/~campbell’’);
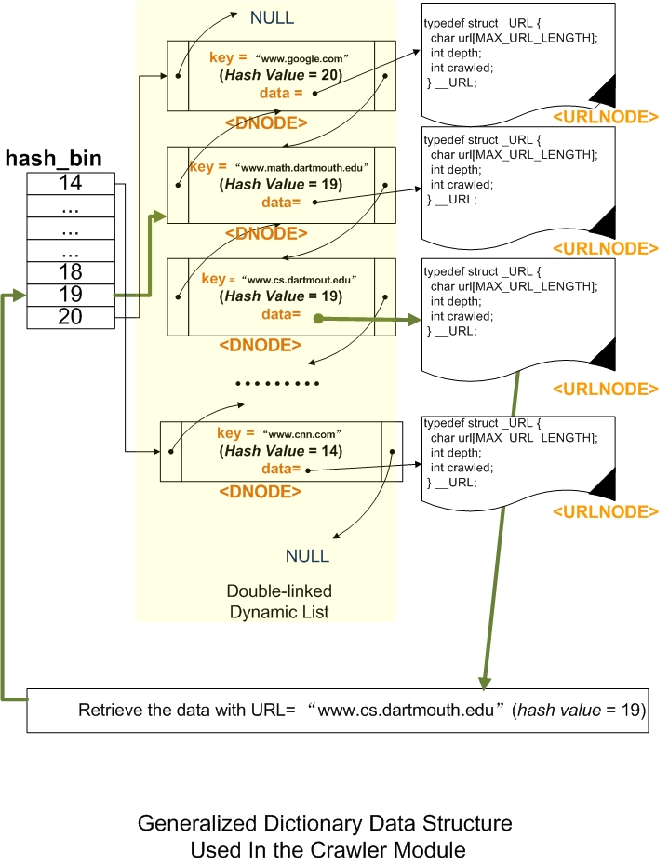
Assume that the hashIndex returned is 19. Then we can say that hash1 will always return 19 for that key. And that the hashIndex indexes a slot in the hash table that keeps a pointer to a DNODE. In our algorithm we can make the following assumption. If the slot contains a NULL pointer (say for the key above) then we are assured that the key is unique. If a pointer is already at slot 19 we cannot conversely say that the URL is not unique because other keys my be hashed at the slot too. So we have to search through the list starting at what is pointed to by slot 19 in the table and search the list until we either find the same URL (therefore it is not unique) OR we come to the end of the DNODEs that are associated with hash value 19. For example, each DNODE holds a key (which in our case is a URL name) therefore assume that there are two DNODEs linked starting from slot 19 with different keys but the hash index 19 (but recall that the hash table simply points to elements in the double linked list). But how do we know that we have got to the end of the list of DNODEs with the same hash value? We recompute the hash value for each DNODE we traverse for the key maintained in the DNODE and if they equal 19 in this case (the same hash index) we know they are related and need to be searched and compared for uniqueness against the current URL. But if the hash index is different (not 19) then we know for sure that the URL is unique and should be linked into the end of the DNODEs that have the same hash value. This paragraph really describes the algorithm for searching using the hash table and hash function. Be sure to read it again before coding it. Be sure to pencil our a few scenarios that help explain the various conditions of searching and insertion. An example of a hash table pointing to DNODES (and DNODES point to URLNODES) is shown in Figure 1.
Now to explain our design choices. The DICTIONARY holds the hash table and the start and end pointers into a double link list. This is an unordered list with the exception that DNODES with the same hash value are clusters along the list at the same place as discussed above. So you hash into the list. Check for uniqueness of the URL If not found add to the end of the cluster associated with the same key/hash value. You will have to search the hash table starting at the hash value and write an addElement function to insert the DNODE into the list at the current place.
prev and next are pointers to the previous and the next element in the dynamic list of DNODEs. start and end are pointers to the first and last element in this dynamic list.
Each element in the dynamic list has a unique string called key. The general use of this data structure is the following: given a key in input, we want to find out an element with the same key. For example, we want to retrieve the element corresponding to a certain URL.
As we said, a linked list, you may have to traverse the whole list, comparing each key of each element to the given key in input. Using a very long list, this process is very slow.
The name hash derives from the fact that it is based on the use of hash functions. These functions return a hash value index that is an integer in a certain range (0 to MAX_HASH_SLOT in our code) given an arbitrarily long string. The longer the string the better.
Each piece of data that has to be stored is associated to a certain position (also called bin or slot) in the list calculated by means of the hash function. For example, by hashing a certain URL, let us say http:\\www.dartmouth.edu), we obtain the position 43. Then the information (i.e., the struct containing the information) is stored in a list associated to the position 43. In fact, different strings in input can be mapped into the same bin; therefore, we do not have a single element associated to this position, but a list of elements.
The goal is to separate the whole list into several parts/sublists (clusters) where each part is composed of one or more elements. Then, the complexity of the search is reduced, since we have to search only through the elements of the list associated to a certain bin/slot retrieved using the hash function.
To implement such a data structure, we keep an array hash in memory, where MAX_HASH_SLOT is the max value of all the possible hash values:
The data structure is allocated in the heap using malloc().
Given a certain string, first you hash1() it, obtaining an hash index h (i.e., the bin in position h, and use the result as the index of the hash array above. The pointer you get from the array points to the first element of the dynamic list characterized by a key equal to h. This mechanism is used to add or retrieve the information. The result of the hash table/function is we only have compare a small fraction of elements associated with the whole list to find the element with the same key rather than search through all the elements - representing a significant speed-up.
The dictionary data structure is quite generic and it can be used with various types of data. Each element not contain only the key but also a data pointer. In our implementation, the data variable stores the pointer (the famous void *pointer) to the data (URLNODE) rather than storing the data itself as in the data structure used for the index. Therefore, users could insert any data in the list simply by providing a unique key and the pointer to the actual data. A generic dictionary is shown in Figure ??. An example of a generalized DICTIONARY hash table pointing to DNODES (and DNODES point to URLNODES) is shown in Figure 1.
In our case, the key is the URL and the data points to a struct of type DNODE. Let us consider the case of the insertion of a DNODE element in this list. The idea is that you have to first find the list with the same hash value by hashing the URL address and then insert your element in the list in the position equal to the hash value (by appending it to the list). If there is no element in the list sharing the same hash value index, you can just insert the element (first element) and change the pointer in the hash array setting it to the memory location of the the newly inserted element. In this case you should add the element to the end of the list (DNODE *end) points to. And, then update the pointer in the hash table at the associated hash index to point to the element. If there is an element, you insert the element at the end of the list assuming no match is found.
url˙list Code snippet for malloc-ing space for a URL, initializing it, linking it into url_list, and then copying the URL over.
URLNODE Code snippet for malloc-ing space for a new URLNODE, initializing its elements, and then copying the URL over.
DICTIONARY Code snippet for malloc-ing space for the dictionary and initializing it - and explicit the double linked list used to hold DNODEs.
DNODE Code snippet for malloc-ing space for the DNODE and initializing it, and adding it to the list - as you can see this is for the condition that there is not other DNODE on the list. The new DNODE is then added to the hash table at the hash index element and the key (URL in this case) is copied over.
Searching for uniquenes of URL. How do we determine that the URL is unique? First we hash into the hash table and if the element is NULL then the URL is unique. We link it into the end of the double link list and update the hash table entry to point to it.
If there is a pointer at the hash index then we do not know if there the URL is unique - why is this the case? We need to search the cluster (defined as the group of DNODES with the same key) to see if there the URL is linked in. We look at the linked URLNODE to do the string compare of current URL againt the URL names in the URLNODES. If we traverse all the cluster and there is no match then the URL is unique and we link it to the end of the cluster.
The figure below shows that the DNODE list as a number of URLs added. The list is searched for the uniqueness of www.sartmouth.edu/˜wpay It is found to be unique and the point in the list is marked where it should be inserted.
url˙list Code snippet for malloc-ing space for a URL, initializing it, linking it into url_list, and then copying the URL over.
Here are the following source files give out to assist in the implementation:
crawler.h- Implementation Spec is captured in the crawler.h file. It defines the important defines, marcos, data structures and prototype functions.
crawler.c- Students add the code starting here. It includes, from the Design Spec (Pseudo code description of the crawler algorithm), inputs and outputs.
Other code given out for the Lab4 (to make your life easier) include:
hash.h- Hash function header file
hash.c- Hash function
html.h- HTML parsing code including GetNextURL()
header.h- Some useful Macros
html.c- GetNextURL()
In the tarball sent you there is also a README file which we point to here for completeness.
README- README