MILESTONE
Reinforcement Learning in Tic-Tac-Toe Game and Its Similar Variations

Group Members: Peng Ding and Tao Mao
Thayer School of Engineering at Dartmouth College

1.What We Have Achieved

We have successfully implemented an algorithm of training the computer to play Tic-Tac-Toe against human. After training, human cannot beat the computer as long as the computer goes first.

Below is how the game-play looks like in the console interface.

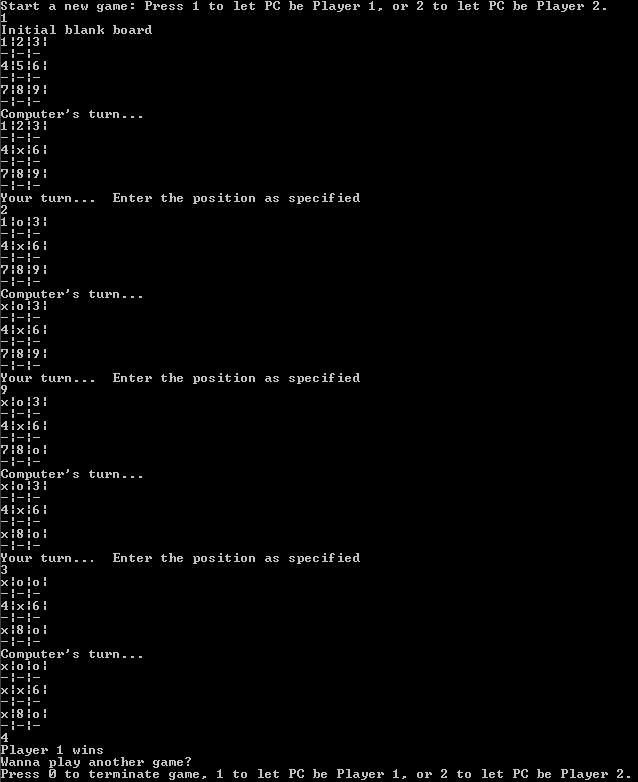
Figure 0 Game-play interface

Here is how the algorithm works to update values for possible states based on reinforcement learning[1]. First, we set up a table of these values. Each value is considered as the recent estimation of the probability that a player wins the game from this particular state. The higher a state value is, the more likely this state leads to a final winning for the player. For each action, a player chooses an available position based on the state values indicating the selection weights. Those state values are learned from the previous learning phases. The two players alternately chooses an available position to fill in untill one player wins the game (three "O" or "X" in a line), or the game reaches a draw. In our implementation, Player "O" denotes human player while Player "X" denotes the computer agent. The advantadges for this setting will be explained below.

For initialization, we set the value of each possible state V(s) to be 0 and the learning rate 0.02.

The algorithm's framework mainly consists of two parts-learning phase and game-play phase. Here follows the brief description of the algorithm's structure:

1. The learning phase currently involves 100,000 learning times. In each episode:
(1) Observe a current board state s;
(2) Make a next move based on the distribution of all available V(s') of next moves;
(3) Record s' in a squence;
(4) If the game finishes, update the values of the visited states in the sequence and start over again ; otherwise, go to (1).

2. The game-play phase make a "greedy" decision based on the learned state values. Every time the computer is making next move,
(1) Observe a current board state s;
(2) Make a next move based on the distribution of all available V(s') of next moves;
*(3) Record s' in a squence;
(4) *If the game finishes, update the values of the visited states in the sequence and start over again; otherwise, go to (1).

*These online afterward learning may not be included in the game-play phase as long as the game strategies are considered to be solid.

2. Convergence of "Afterstate" Value

Player "X" represents the computer and Player "O" represents human. Player "X" goes first. We will show the convergence of "afterstate" value using the following example.

Which position is chosen to be the opening position is very crucial for Tic-Tac-Toe game. The choice of central position results in "no-loss" guarantee, which is easily verified. Therefore, the computer should be able to find the great value of opening in the center. Below is the figure showing the convergence of the values of nine opening positions including the center.

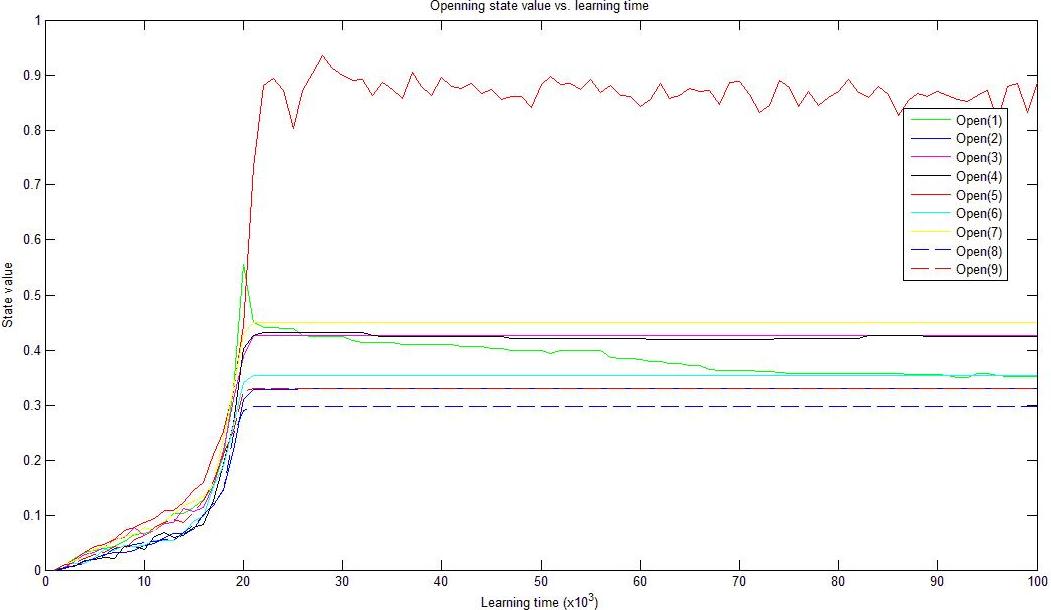
Figure 1 Convergence of nine opening positions: the central position is the best choice.

Assume that the computer chooses the center for opening and the game has reached state S1, as shown in Figure 2. Now it is again player "X" 's turn. Obviously, chance of winning the game is greater if player "X" takes the position of 1,3,7 or 9 (Figure 2).

Figure 2 Board state S1

We assume that the computer has been trained enough to choose an action/position leading to a higher state value as, now, Player "X" chooses position 1 shown in Figure 3.

Figure 3 Board state S2 after Player "X" takes position 1

The plot below shows that the afterstate value of state S1 vs. learning time (Figure 3). The value converges to approximately one. It explains that after enough time of learning Player "X" knows winning from state S2 is almost guaranteed.

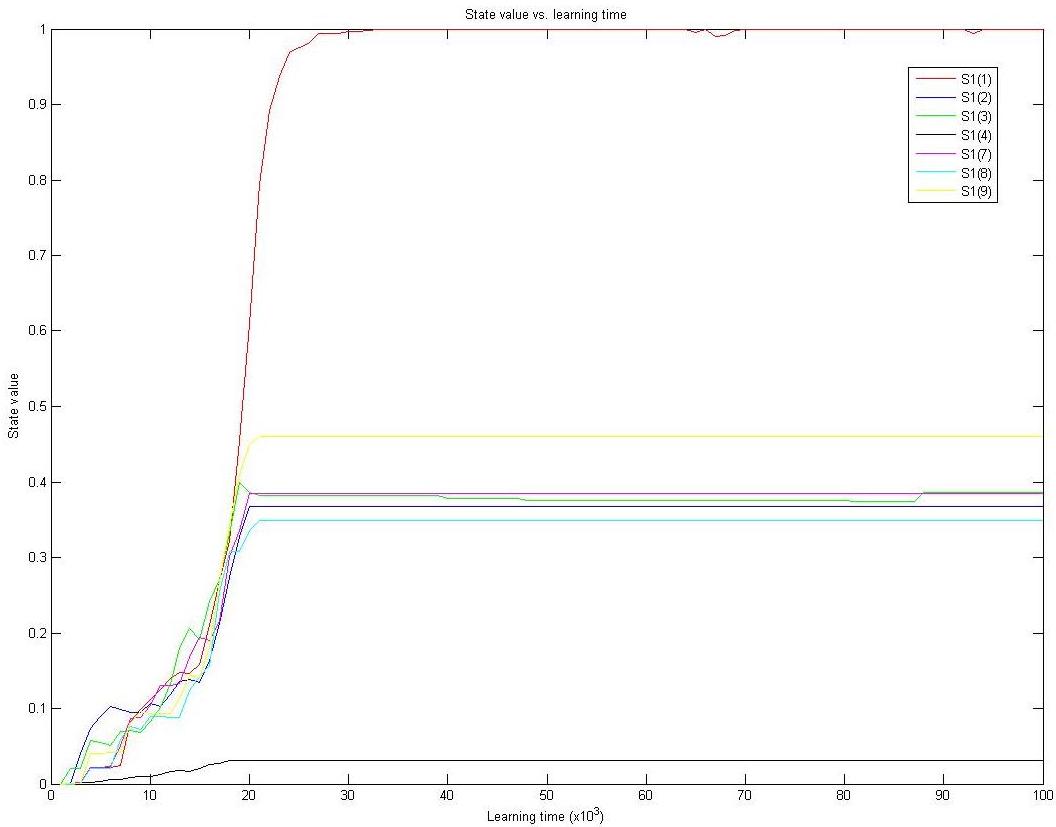
Figure 3 Afterstate values of state S1 vs. learning time

Then Player "O" chooses position 9 to avoid losing the game (Figure 4). In the next step, a well-learned player "X" (computer) will choose position 3 (Figure 5).

Figure 4 Board state S3 after Player "O" takes position 9

Figure 5: State S4

Up to this point, a well-trained (after sufficient learning time) computer, Player "X", will win the game no matter what position Player "O" takes. More specifically, If Player "O" chooses postion 2, Player "X" will takes position 7 to win the game. If Player "O" chooses postion 7, Player "X" will takes position 2 to win the game. If Player "O" chooses postion 4 or position 8, Player "X" will win the game by either taking postion 2 or postion 7.

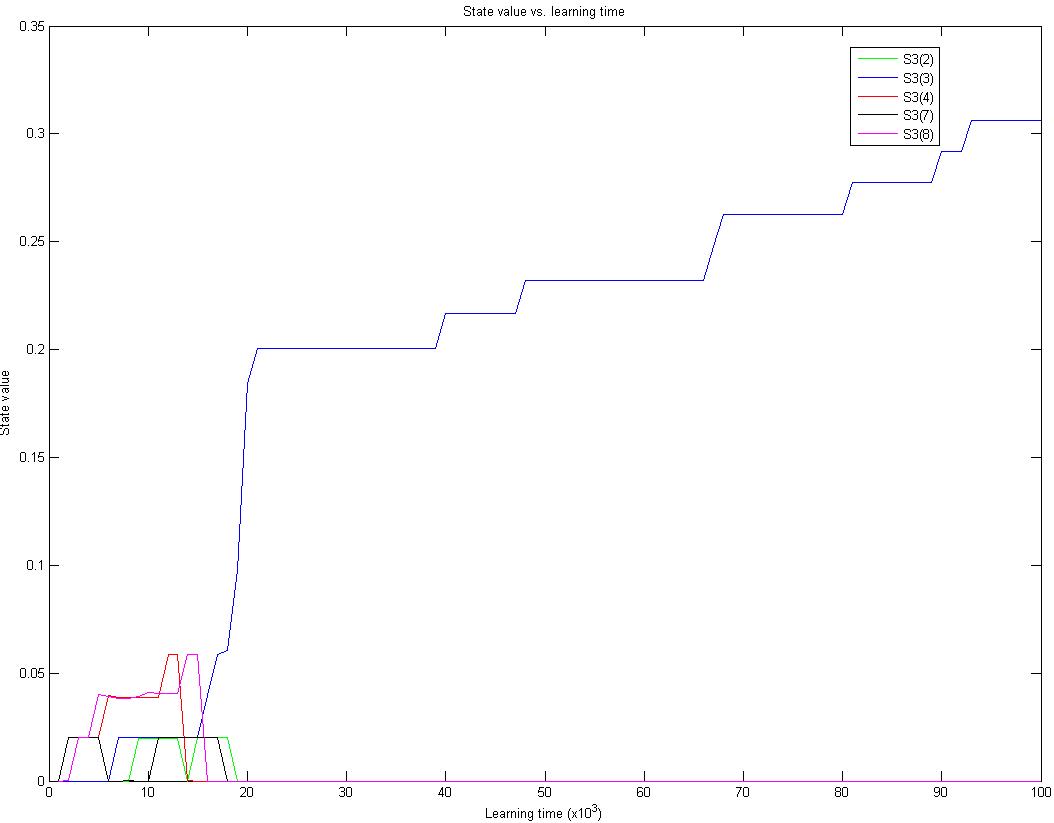
Figure 6 Afterstate values of state S3 vs. learning time

Figure 6 shows how afterstate values of S3 converge over time. We notice that the true value of the crucial state does not quickly converge to the real value (i.e. one) due to the insufficient learning time. However, it will not prevent the algorithm make a right decision in game-play because the value of the crucial state stands out compared to those of others'.

3. Self-Play Learning Phase

As the project proposal states, "self-play training method" is that two computer agents play against each other and learn game strategies from simulated games. This training method has several advantages such as that an agent has general strategies rather than those associated with a fixed opponent. Self-play training method may have a slow convergence rate of state values in some algorithms, especially in the early learning stage [2]. However, it works well in our algorithm because the scale of the problem is not too large. In other words, the computer player will gain fruitful learning experience and update his state values based on various successes and failures even though we initialize the value for each possible state as zero. It will take us much longer time if we train the computer agent ourself by human-computer interaction. On the other hand, we do not bother to train the computer agent ourself since it will take us quite a long time to do so.

References

[1] R. Sutton and A. Barto. Reinforcement Learning: An Introduction, MIT Press, Cambridge, MA: pp. 10-15, 156. 1998
[2] I. Ghory. Reinforcement learning in board games, Technique report, Department of Computer Science, University of Bristol. May 2004
[3] Thanks to Boulter.com/ttt/. Illustration figure source.