The goal of this project is to apply linear regression (in particular, locally-weighted) and neural networks to predict binding energies of a chemical system with a particular spatial arrangement of atoms. It is essentially a problem of interpolation, to infer new data points given a spread of training data. The goal is to construct an energy profile (surface) which maps the heights (z-coordinates) of lowest energy for any given (x,y) coordinate.
In computational chemistry literature, the most prevalent method for interpolation of quantum calculation results is neural networks. My goal is to compare the performance of neural networks with linear regression, and to measure the overall reliability and robustness of such interpolation methods in practice.
An algorithm for regularized least squares linear regression and a version of locally-weighted linear regression have been implemented. This locally weighted linear regression algorithm finds the k nearest training examples and performs least squares regression using those closest examples as the training data. The motivation for this sort of approach is primarily simplicity, as it is similar to applying a very narrow Gaussian weight function.
One question of interest pertains to how much information should be included in the input vectors. The simplest case is to simply have the coordinates of the oxygen atom (the only one that moves). However, it is possible to include the coordinates of the gold atoms as well. I have implemented code to build the feature vectors to consist of the oxygen coordinates plus the coordinates of the k nearest gold atoms.
Using a small portion of the training set (2059 examples), some preliminary results were obtained for the purpose of parameter optimization (via cross validation). For regularized least squares linear regression, using a linear basis set, Figure 1 was obtained from cross-validation by varying the number of gold atoms included in the input vectors. The more nearest gold atoms included, the better performance was. A similar result was observed for locally weighted linear regression (Figure 2). Interestingly, the cross-validation score for regularized least squares regression is slightly better than that for locally-weighted linear regression.
Figure 1:
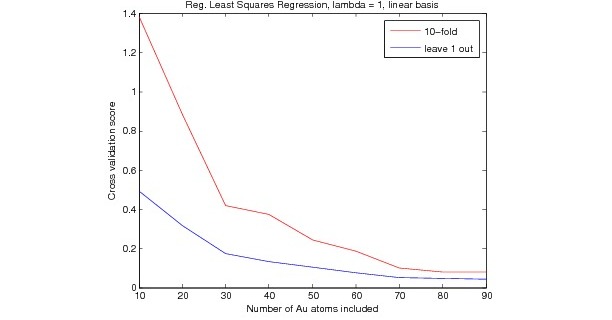
Figure 2:
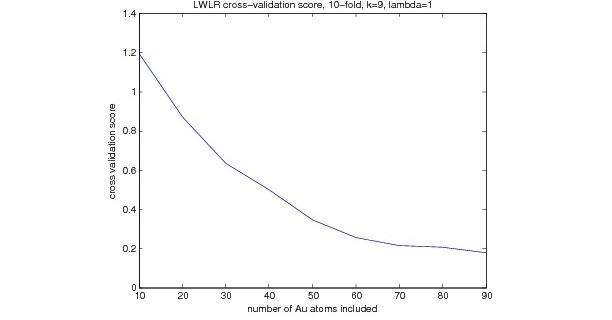
Both above results use a linear basis function, but using a nonlinear basis function should improve the result. Using 90 gold atoms means that the input vector contains 91 coordinate triplets, or 183 dimensions. Thus, using a nonlinear basis function will drastically impact the computing cost, particularly for locally weighted regression (which must compute Euclidean distances between the test vector and every vector memorized). In general, for this particular application, locally-weighted regression has serious cost disadvantages compared to linear regression due to the dimensionality and large number of examples that would be memorized (order of thousands or ten-thousands). In retrospect, LWLR was probably not a wise choice for this application, given the above cost issues, and given performance that is not apparently improved over non-weighted linear regression, though this also may indicate that further tuning is required.
On the other hand, even high-dimensional locally-weighted regression would still be faster than performing the actual quantum calculation for one data point, which requires a supercomputer and takes 15-20 minutes for the simplest models of this system.
Goals completed:
Goals not yet completed
Implementation Tasks:
Analysis Tasks: