Thus far I have focused on compiling a library of known instruments which will be used to identify instruments in previously unheard recordings. This library consists of a number of centroids of extracted harmonic structures for each fundamental frequency (within an instrument's range) for each instrument in the library
The first step in compiling this library was obtaining data. I used audio files from the University of Iowa Electronic Music Studios Musical Instrument Samples. These samples were converted to wav files and read into matlab where they were split into single note samples before harmonics were extracted.
Extraction of harmonics was accomplished using the spectrogram funcion in matlab. This computes a discrete Fourier transform of the time-domain signal broken into many overlapping segments convoluted with a hamming window. The log of the output frequency-domain signals are analyzed at each time step.
Analysis of a frequency-domain signal occurs in two steps. Firstly, a smoothed envelope is fit to the signal by convoluting the signal with a discrete Gaussian kernel. Secondly, local maxima of the signal which are above the envelope by a certain threshold (8 dB) are identified as potential peaks. The first large peak is labelled as the fundamental frequency and is used to guide the rest of the extraction process.
We expect to find peaks at integer multiples of the fundamental frequency so for each of these multiples from two through twenty we consider only potential peaks within a small window around this expected value. If there is more than one potential peak within this small window a choice is made using a Gaussian 'likelihood' function based on distance from expected value and amplitude of the peak.
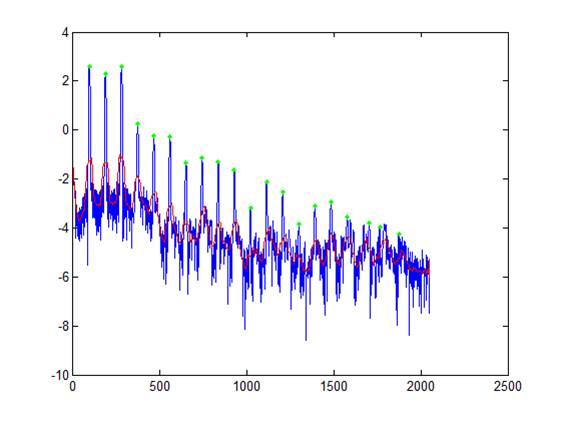
The normalized spectra extracted from each time step across all dynamics (pp, mf, and ff) are fed into k-means with k = 10 and the centroids are stored in the library.
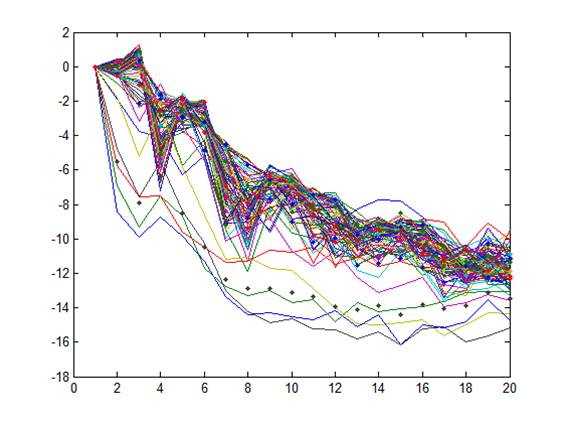
Within the next two weeks I will test the accuracy of this technique using the k-nearest neighbors algorithm. Depending on these results I may try to add additional classifiers such as attack and release envelopes. From here classification of two or more instruments will be attempted.
Upon satisfactory completion of the instrument identification phase I will begin the separation phase. This will be accomplished using maximum-likelihood estimation of fundamental frequencies followed by extraction of relevant features. Features will be used to indentify instruments present and this information will be used to correct missing or overlapping harmonics in the extracted features.
Individual instrument tracks will be obtained by reconstructing the extracted harmonics via an inverse Fourier transform using the overlap-add technique. This may require phase estimation of the separated signals. For the two-instrument case a second reconstrution for each instrument can be formed by taking the difference of the original signal and the reconstructed signal of the other instrument.