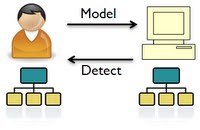
Deqing Li Introduction In my own research project "deception detection" [1], we use Bayesian Networks (BNs) to simulate a group of human experts since their reasoning processes can be represented as the inference over BNs. Deception detection is achieved by predicting the answers of each BN and comparing the predicted answer with the deceptive answer from experts. In this project, an alternative way to detect deception by machine learning is proposed. Specifically, we first simulate human experts by BNs and then learn their BNs from the observations generated from the original BNs. Thus the original BN serves as a simulator of an expert and the learned BN as a model of the expert. To test the reliability of the experts' answers to given evidence, we reason through the model and compare the answers with the experts' answer inferred from the simulator. An achitecture of the system can be depicted as Figure 1.  Fig. 1 Achitecture of Deception Detection by Learning Bayesian Networks Method
To Learn a BN, one needs to specify two things: the structure of a BN and the parameter (conditional probability table) of a BN [2]. Both can be learned from observations. For example, to learn a BN with random variable (r.v.) A, B, C, observations such as {A=1, B=2, C=3} and etc. can be used to learn the CPT given the structure or to learn the structure itself. The observations are randomly generated from the simulator BNs. However, learning the structure of BN is much harder than learning the parameter, and learning with incomplete data is harder than with complete data.
With complete data, learning the CPT is as simple as maximizing the likelihood of the observations [2].
 where xi[m] denotes the ith r.v. in the mth observation, and pai[xi] represents the ith parent of xi.
Incomplete data means
that some r.v.s are hidden from the observations. In this case, we use
Expectation-Maximization (EM) Algorithm [3] to learn the parameter. EM
algorithm is used to find the maximimum likelihood of parameters of
statistical models based on unobserved data. It is composed of an E
step and an M step. In the E step, we calculate an expected value of
the log likelihood based on an estimation of the unobserved data, while
in the M step, we find the parameter that can maximize the log
likelihood. The EM steps improve the log likelihood while iterating and
achieve an optimal when it converges. [4]
The traditional way
to learn the structure of a BN is to search through the structure space
for one that can maximize the posterior probability of the structure
given data.
 Timeline Week 1: Implement the code to randomly generate observations from simulating BNs (both complete and incomplete). Week 2: Implement the algorithm to learn parameter from complete data Week 3: Study EM algorithm and how to apply EM algorithm to learning BN Week 4: Implement the algorithm to learn parameter from incomplete data Milestone Presentation Week 5: Test the learned BN by reasoning with random evidence Week 6: Implement the heuristic to detect deception Week 7: Finalize and Work on the report References [1] E. Santos, Jr., D. Li, and X. Yuan, “On deception detection in multi-agent systems and deception intent”, in Proc. SPIE, Orlando, FL: SPIE, March 2008, vol. 6965. [2] K. Murphy, "A Brief Introduction to Graphical Models and Bayesian Networks", http://www.cs.ubc.ca/~murphyk/Bayes/bnintro.html, 1998. [3] A. P. Dempster, N. M. Laird, and D. B. Rubin. "Maximum likelihood from incomplete data via the EM algorithm". Journal of the Royal Statistical Society B 39, 1–39,1977. [4] Lauritzen, S. L. "The EM algorithm for graphical association models with missing data". Computational Statistics and Data Analysis 19, 191–201, 1995. [5] N. Friedman, and D. Koller. "Being Bayesian about network structure: A Bayesian approach to structure discovery in Bayesian networks". Machine Learning 50, 95–126, 2003. |
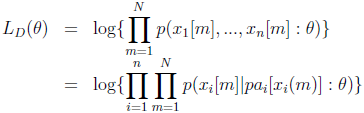
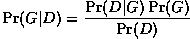
_text_