As we said, in order to model conversations, we want to find
causes that influence human conversations. There can be many influences on somebody's conversations, and social tie is one of them. As an example of other types of influences, we can say whether somebody will be in a conversation at time 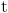 largely depends on whether she is in
a conversation with a talkative person at time largely depends on whether she is in
a conversation with a talkative person at time 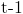 . .
Although we are predicting human conversations
using social networks, we want to use both the information of talkativeness
of a person and social ties.
We are doing so because we would like to quantitatively explore the contributing factors in somebody's conversations due to the influence of social network and due to speaking with a talkative person.
This sort of discrimination helps us to find appropriate
channels when we want to pass sensitive information to somebody.
In this project, we know the social network structure as a priori, and the social network was derived from bluetooth proximity,
previous conversations and self-reported surveys. From our dataset, we also know whether somebody is talking or not at a given time.
Then we can find conversations using techniques described in
[2].
We will model human conversations using
multiple interacting Markov
chains. We will be using the boolean variable 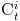 which is 1 when subject which is 1 when subject 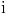 is in conversation at time is in conversation at time 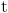 and 0 when she is not. Let us consider conversations between
and 0 when she is not. Let us consider conversations between 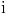 and and  . Now, to predict whether . Now, to predict whether 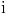 is
in a conversation at time is
in a conversation at time 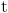 , we will be modeling , we will be modeling 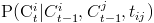 , i.e., the probability of , i.e., the probability of 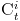 conditioned on conditioned on 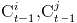 , and the social tie strength between , and the social tie strength between 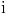 and and  denoted by denoted by 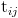 .
To compute the high-dimensional conditional probability table needed for .
To compute the high-dimensional conditional probability table needed for 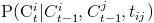 , we will be using
the Saul and Jordan [1] proposed method, where one variable conditioned on many others is approximated as a convex combination of the pairwise conditional tables. We use their approach and model , we will be using
the Saul and Jordan [1] proposed method, where one variable conditioned on many others is approximated as a convex combination of the pairwise conditional tables. We use their approach and model 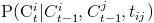 as mixture of conditional distribution as follows: as mixture of conditional distribution as follows:
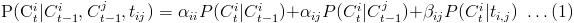
We will learn the parameters of (1), which we call the
influence parameters, such that it maximizes the
likelihood of our data. The parameters thus learnt will give us
appropriate influence level for a specific social tie. However,
inferences using this model is very challenging because
inference even in a normal Markov chain is of quadratic complexity,
and coming up with a inference algorithm for a fairly general
dependency structure as (1) is even more challenging, which we will be attempting to solve in this project. |