The Problem Revisited

0.1 HMM

Automatic Playlist Generation (APG) aims to suggest an appropriate sequence of songs that retains listener interest. Online music distribution services such as Last.fm are generally motivated to keep their users’ attention so that content providers may sell music-related services or products, such as albums or ringtones.

Given that a music database may be large (on the order of millions of songs) and that a user’s musical preferences unknown, it is challenging to generate optimal music sequences. Previous approaches generally rely on similarity metrics (either content or metadata based) or user preference modeling. This project attempts to model the music sequencing found in professionally produced albums. Commercially sold albums are sequenced by experts in music marketing and music production. Song sequences in albums therefore encode expert knowledge.

In my proposal I suggested that I would use HMMs to capture such knowledge. HMMs (which are thoroughly described in [1]) are an often-used class of latent variable model which capture first-order Markov chain dependencies. An HMM allows one to model the transition probabilities for z discrete hidden states by looking at the observable state emissions. HMMs are often used with sequential data.

In particular, the hidden states of a music album are the song transitions. The observable emissions are in the form of content-based real valued descriptors of the song. Give the state emissions, I wish to learn the hidden states that are the song transitions.

The HMM requires one to provide the number of hidden states that exist in the data. If too few states are given, then the data may be under-fitted. Likewise, an inappropriately large number of states can result in over-fitting. This project’s application scenario makes it difficult to choose the correct number of states. We do not know how many “types” of song transitions there are. I therefore also suggested that I would implement the Infinite Hidden Markov Model as proposed in [2].

1 Progress

The data has been organized into 8889 song sequences of 5 songs each. Each song is characterized by a 52-dimensional real valued vector comprised of:

• The tempo in Beats Per Minute (1).
• The duration in seconds (1).
• The fade-in time in seconds (1).
• Timbre features for the first 20 seconds of the song (12).
• Chroma vector energies (pitch class energies) for the first 20 seconds of the song (12).
• The fade-out time in seconds (1).
• Timbre features for the last 20 seconds of the song (12).
• Chroma vector energies (pitch class energies) for the last 20 seconds of the song (12).

Following a conversation with Lorenzo, the data was standardized so that each dimension has zero mean and unit variance.

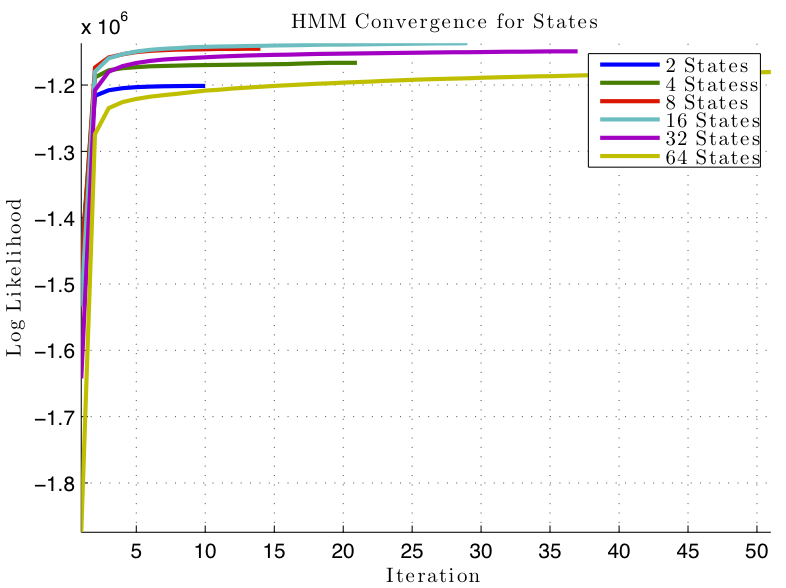
I trained separate HMM models using a single Gaussian as the observation model on state space sizes of 2, 4, 8, 16, 32, and 64. each 52-dimensional gaussian was initialized with k-means over each state. The Gaussians were full-covariance. Note: I incorrectly reported that the observation model was a Mixture of Gaussians. After class, I confirmed that the actual observation model was a single Gaussian.

The iteration time and log likelihood for each model are shown in Figure 1. I found that it took relatively few iterations to reach convergence. I reported in class that the model tended to converge to one state. However, after I standardized the data, the model converged to varying probabilities over all states.

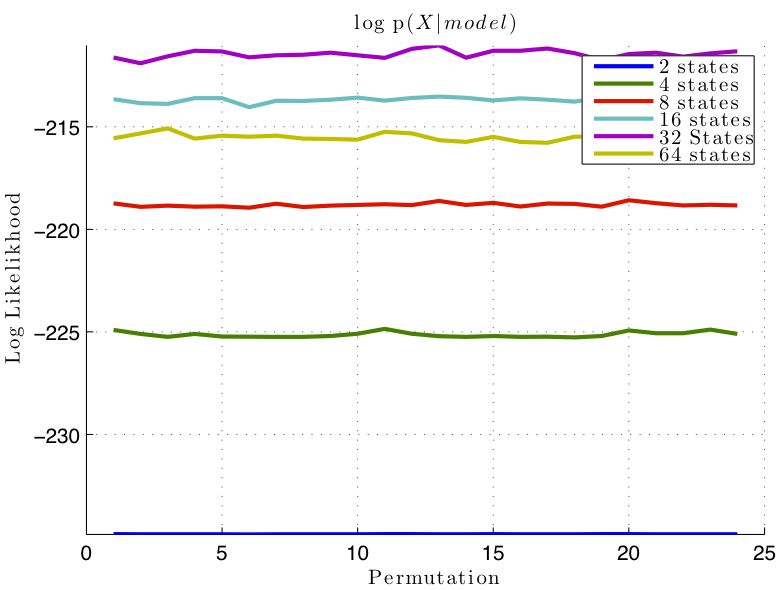
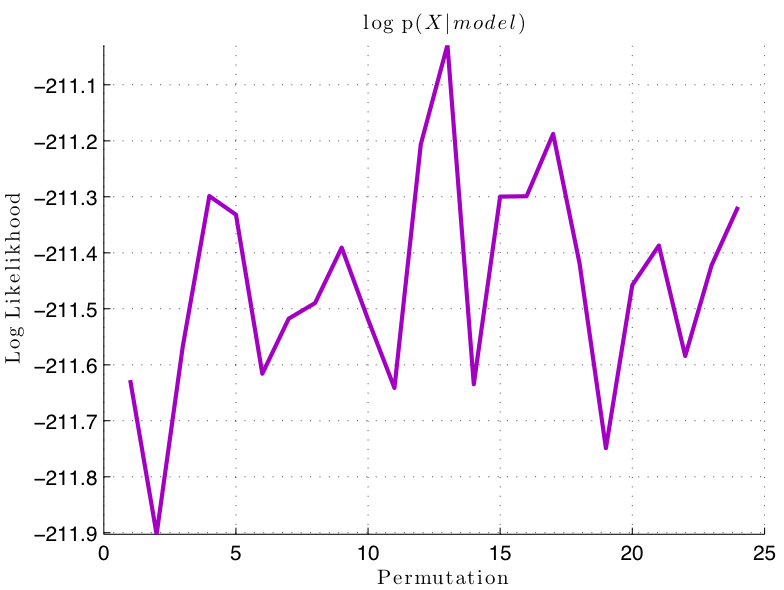
I tested the data on 4889 unseen album sequences for each model. In order to test the accuracy of each of the models, I created permutations for each song sequence, holding song number 1 constant. Therefore, each of the 4889 album sequences was expanded to 24 album permutations, including the ground truth. I hoped that the best model would show the highest median log likelihood over the ground truth album sequence, compared too the permutations. Figure 2 shows that the models did not perform as desired.

1.1 Nonparametric HMM

I spent a considerable amount of time absorbing the literature on nonparametric HMMs and am still having difficulties digesting the material. At first, I begin to implement [2]’s algorithms for the infinite HMM. Then I became aware of HDP-HMMs, which use a Hierarchical Dirichelet Prior on the State and and observation models [3]. Finally, I became engrossed in Emily Fox’s adapted version, which uses a “sticky” parameter to state encourage self-transition [4, 5, 6].

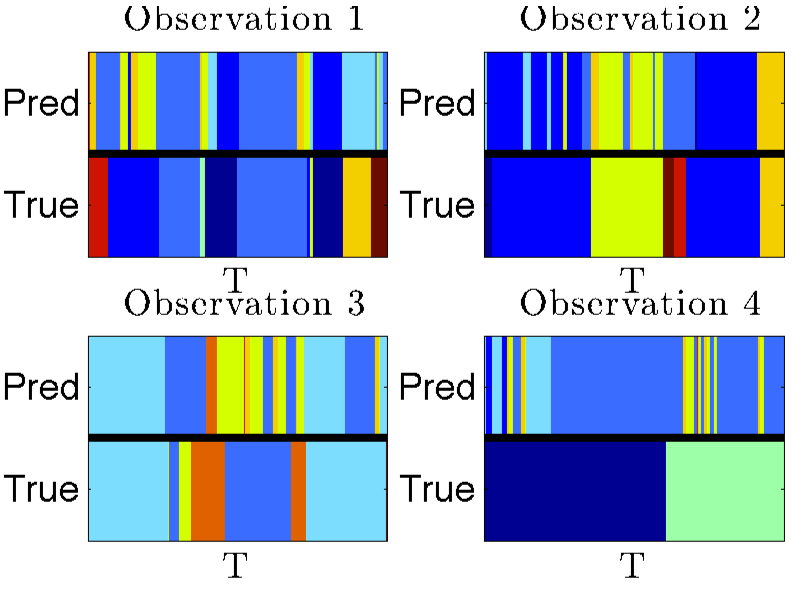
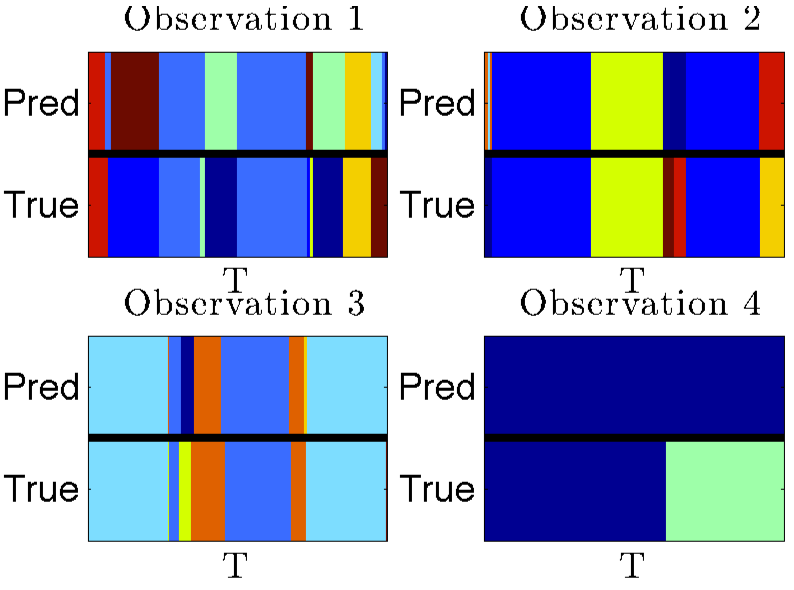
I was able to generate some synthetic data (using some code provided on Emily’s web site) and test the HDP-HMM. Figure 3 shows a toy example of 4 observations with sequence length T = 500. The top four graphs show the initial model predictions for the four observations, and the bottom four graphs show predictions after 2 2000 Gibbs samples.

I am still having much difficulty understanding the algorithms, and there are multiple hyperparameters to set in their current instantiation. I have started a training run across the full dataset, but the computation is prohibitively slow for any cross-validation of models. (At last check, the model had taken about 12 hours to reach 600 iterations of the Gibbs sampler. The literature reports for 30,000 to 50,000 iterations of the Gibbs sampler on successful models.)

2 Future

After today’s conversation with Lorenzo, it is clear that I need to focus my attention away from the HDP-HMM for the time being. The next steps will involve reducing the Gaussian covariance matrix to diagonal or shared covariance; and trying dimensionality reduction methods. I have also thinking about clustering the data into song types (either by content, tags, or both) and training HMM models for particular song classes. If I get more satisfying results on the HMM, I will return to the HDP-HMM or try a Linear Dynamical System for comparison.

References