Automatic Playlist Generation (APG) is an algorithmic means for grouping and ordering music. APG systems are an integral part of automatic music recommendation systems; they generate sequences of songs and aim to maximize the listening time of their subscribers. Successful APG is non-trivial; generating a sequence of songs based on maximizing music similarity runs the hazard of producing boring arrangements. When adjacent songs sound too similar, listeners may lose interest quickly. It is therefore important that adjacent songs preserve controlled novelty in APG systems. Various methods for retaining listener interest have been implemented in the past, such as requiring adjacent song similarity scores to remain below a threshold, or by providing a means for users to train the system through feedback. Such methods of APG optimization may be cumbersome, may assume that the user has high level knowledge of his or her preferences, or may overemphasize the importance of music (dis)similarity.
Music albums are meticulously fashioned by their producers to maintain the attention of their listeners. An album sequence, which is usually composed during the mastering stage of music production, is engineered so that it promotes momentum, continuity, and enjoyment. Albums share a similar revenue model as other forms of music distribution; if an album cannot retain listeners’ attention, it is unlikely to be profitable, especially when the option to purchase individual songs exists. The knowledge encoded by transitions between songs is hidden from ordinary music listeners. However, by observing sequences of songs, we may be able to learn this knowledge.
This project will use album sequences and content-based features to model the transitions between songs in commercially available albums. Two approaches based on the Hidden Markov Model will be implemented and evaluated: parametric and non-parametric. The hidden states of the HMM will represent the types of transitions that exist between two songs. HMMs are well-suited for modeling short-term temporal dependencies, and I therefore feel that HMMs are an appropriate model to investigate.

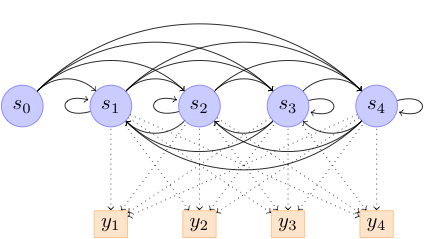
First, I will build a fixed state parametric HMM using a subset of the features discussed below. The aim is to build a model that captures the transition types as hidden states. Figure 1 shows such a model, in which 4 hidden states represent the types of transitions that may occur between any two songs. The observable data will be song-level and transition features. The number of possible feature combinations is large, so I will perform feature selection and/or dimensionality reduction. However, I am not yet sure which methods to use.
As a pilot study, I have already tried HMM modeling on a portion of my dataset with a limited feature set. My results were above chance, but not satisfactory. I believe feature selection on a larger feature space will greatly improve the model. I did not use any timbre-based features in my initial model and many of my features were coarsely quantized. In addition, I made some weird design choices in my initial experiment, which I will correct in this round. For instance, I discretized the observation data using GMMs, which was probably an unnecessary step.
By using an ordinary HMM, one assumes that there are a finite set of transition types (states) that can be modeled in albums. However, this is a strong assumption to make, given the extent of music genres that exist. To extend my model, I will implement an Infinite Hidden Markov Model, as described in [1]. The Infinite Hidden Markov Model uses a two-level Hierarchical Dirichlet Process to define a non-parametric HMM. As such, it might be more appropriate than a fixed state parametric HMM.
Both models will be evaluated based upon their ability to generate the correct sequence of songs in an album from one or more random seed songs. For instance, if the model is given songs 2 and 3 (from the same album) as initial input, the model should generate a sequence of states that are similar to those of the actual (unseen) album sequence.
Columbia University’s LabRosa recently released the Million Song Dataset (MSD) [2]. The MSD is a comprehensive corpus of songs that were chosen by LabRosa based on criteria such as familiarity, tag prominence, cross-availability with other datasets, and extreme values. The song metadata and analysis features in the dataset are generated by the Echo Nest API1 . There are few datasets available to the Music Information Retrieval community that include full or partial albums across multiple genres and artists; the MSD thus provides a unique opportunity to model album-based information. Table 1 shows the data fields included with the dataset.
| Million Song Dataset Fields
| ||
| Analysis Sample Rate | Artist 7digitalid | Artist Familiarity |
| Artist Hotttnesss | Artist Id | Artist Latitude |
| Artist Location | Artist Longitude | Artist Mbid |
| Artist Mbtags | Artist Mbtags Count | Artist Name |
| Artist Playmeid | Artist Terms | Artist Terms Freq |
| Artist Terms Weight | Audio Md5 | Bars Confidence |
| Bars Start | Beats Confidence | Beats Start |
| Danceability | Duration | End Of Fade In |
| Energy | Key | Key Confidence |
| Loudness | Mode | Mode Confidence |
| Release | Release 7digitalid | Sections Confidence |
| Sections Start | Seg Confidence | Seg Loud Max |
| Seg Loud Max Time | Seg Loud Max Start | Seg Pitches |
| Seg Start | Segments Timbre | Similar Artists |
| Song Hotttnesss | Song Id | Start Of Fade Out |
| Tatums Confidence | Tatums Start | Tempo |
| Time Signature | Time Signature Conf | Title |
| Track Id | Track 7digitalid | year |
|
| ||
Track numbers and total track counts are not included in the MDS. However, each song in the corpus includes 7digital2 IDs for artists, albums, and songs, if they exist. 7digital has provided me XML dumps of their American and British catalogues for this project. The combined 7digital catalogues incorporate 316,702 distinct artists; 884,291 distinct albums; and 970,7168 distinct songs. Out of these, I have found 341,544 songs that are also in the MSD. Out of this subset, I have searched for all albums with the first 5 contiguous tracks also existing in the MSD. This query has left me with 44,445 songs across 8,889 albums and 5,076 unique artists.
I’ve outlined a proposed timeline to reach a milestone. If possible, I would like to submit partial work on this project to the 12th International Society for Music Information Retrieval (ISMIR) Conference. The conference submission deadline is May 6, which is early relative to our class schedule. Towards meeting my objectives, I will focus primarily on parametric learning up until the submission deadline. My conference paper would therefore lack evaluation of a non-parametric model. However, my final class project will include the non-parametric model along with a comparative analysis of performance against the parametric model.
| Date | Objective |
| April 19 | Organize data. The data set is too large too be processed locally. I will be using MYSQL for data indexing and all processing will be performed on the Discovery cluster. |
| April 26 | Perform feature analysis and selection. |
| May 3 | Implement and evaluate parametric HMM with fixed number of components. |
| May 6 | ISMIR submission deadline. Prepare paper for submission. |
| May 10 | Milestone. Show complete or near-complete experimental evaluation of parametric model. Show preliminary results on non-parametric model. |
[1] M. Beal, Z. Ghahramani, and C. Rasmussen, “The infinite hidden Markov model,” Advances in Neural Information Processing Systems, vol. 1, pp. 577–584, 2002.
[2] T. Bertin-Mahieux, D. P. Ellis, B. Whitman, and P. Lamere, “The million song dataset,” in Proceedings of the 11th International Conference on Music Information Retrieval (ISMIR 2011), 2011. (submitted).