We address the problem of handwritten character recognition. There are numerous applications in which automatic detection of handwritten characters and digits would have tremendous utility. One example is that of automatically recognizing characters in hand-printed forms [3]. By applying modern machine learning techniques like neural networks to this problem, we achieve error rates under 5%. In particular, we consider back-propagation networks.
We use the MNIST (mixed NIST) database which, as the name implies, is a mixture of two different databases, NIST-SD 1 and NIST-SD 3 (MATLAB version acquired from [2]). It comprises a total of 70,000 greyscale images of digits with corresponding labels: 60,000 for training and 10,000 for testing. Raw images were normalized to occupy a 20 pixel x 20 pixel bounding box. These were then centered to fit inside a 28 pixel x 28 pixel via center of mass computations. The data set itself has been used in numerous papers over the years and seems to be a good choice.
It may be worth mentioning that the first 5,000 test samples of MNIST are supposed to be easier to classify than the last 5,000. This is because the first 5,000 samples were taken from NIST-SD 3, a database of digits written by Census Bureau employees, while the last 5,000 were taken from NIST-SD 1, a database of digits written by high school students. This discrepancy in perceived ease of classification also seems as if it would be interesting to look at, though we do not explore it here.
Above is an example of entries in the MNIST database.
Below we list some benchmarks for misclassification error by which we can compare our results to. An extensive list of benchmarks can be found at [1].
k-NN: 5.0% error
SVM: 1.4% error
Neural Networks: 4.7% error
Convolution Networks: 1.7% error
k-NN: 0.63% error
SVM: 0.56% error
Neural Networks: 0.39% error
Convolution Networks: 0.23% error
We approach the problem with back-propagation networks. [5] and [6] provide good primers on the subject. Multiple architectures for back-prop networks have been used in the literature. We consider back-propagation networks of 1 and 2 hidden layers respectively. The 1-hidden layer back-prop network we tested comprised 784 input nodes corresponding to each of the 28x28 pixels, 300 hidden nodes, and 10 output nodes corresponding to each of the 10 digits. The 2-hidden layer back-prop network we tested comprised 784 input nodes, 300 hidden nodes in the first hidden layer, 100 hidden nodes in the second hidden layer, and 10 output nodes. For our second hidden layer we were suggested to try 40 hidden nodes instead of 100, but our results were not as good, so we stuck with 100 nodes.
For our activation function, we use the familiar sigmoid function [13]:
![]()
Our implementation employs the technique of gradient descent for back-propagation. Our general back-prop algorithm is summarized in [12]. The back-propagation networks we used were trained over multiple epochs using both a fixed and dynamic log-scaled values. We also analyze misclassification on a per digit basis. Additionally, there is code available to perform the tests using k-nearest neighbors.
After implementing the basic structure of our ANN, we experimented with various alpha (step size) values and epochs. We've have had the most success with an alpha value of 10^-3. The training error for both the one hidden layer and two hidden layer neural networks are shown below.
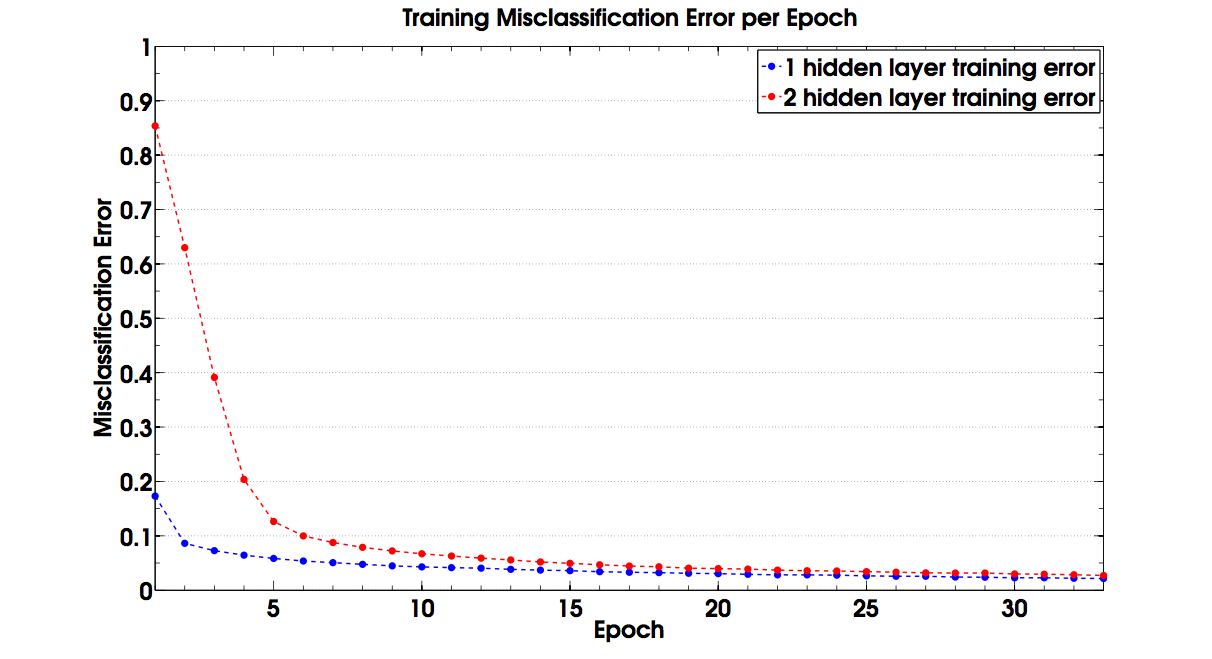
For the single hidden layer neural network, we achieved 3.1% error after 33 epochs. For the two hidden layer neural network, we achieved 3.76% error after 33 epochs. It may be a bit surprising that one hidden layer performed better than two. One reason is that we never converged. We were still making significant progress on both the one hidden layer neural network and the two hidden layer neural network after 33 epochs, but there was far more progress per epoch with the two hidden layer neural network. The role the lack of convergence plays in two hidden layers is also compounded by the fact that the ratio between the training error on the last epoch run and the test error is closer to one for the case of two hidden layers. In short, this means that converging makes a bigger impact on the two hidden layer neural network.
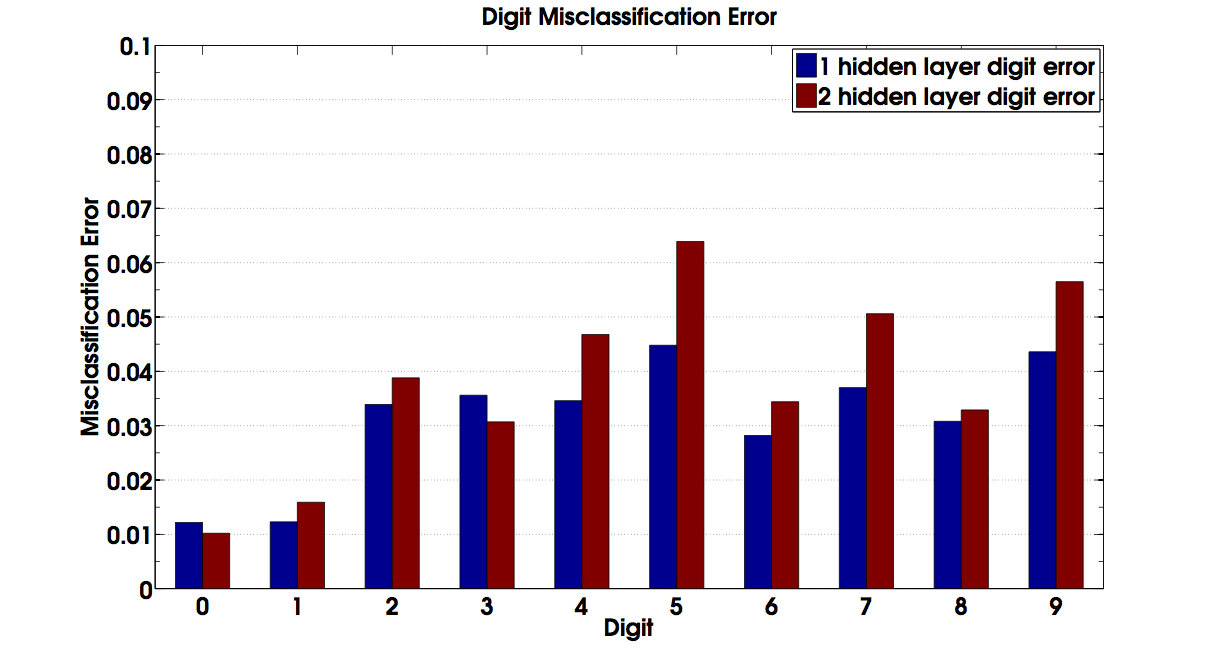
Digit misclassification errors for the neural networks can be seen below. We see roughly the same shape for both neural networks. The digits 5 and 9 seem to be misclassified the most as one might expect. 5 is likely to be mistaken for a 6, 3, and 8. A 9 may often be misclassified as an 8 or a 3. We also don't see very much error with 0 or 1 as one would expect.
We also tested the simple k-NN classifier. However, we didn't have much time after implementation to run tests, so we instead took a per digit randomized subset of one fourth of the test examples. We achieved a misclassification ratio of 3.4%. While this is obviously a bit unreliable as we didn't use the whole test set, it is a good indicator of how the whole test set would perform. The per digit errors are given below.
I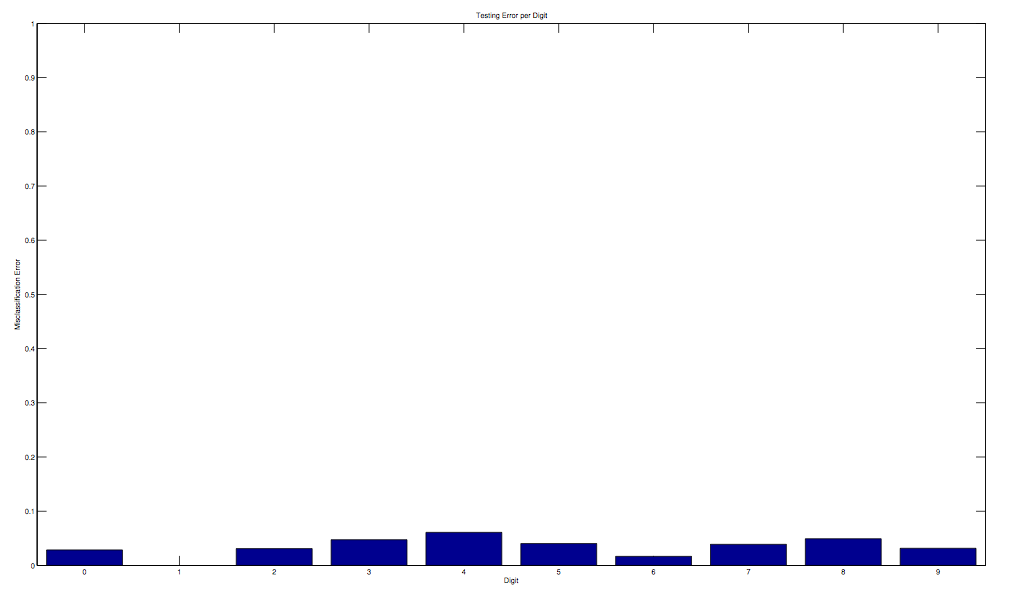
We also looked at shape context matching, but did not apply them for a few reasons. One reason is that the algorithm seems far more suitable for a k-NN classifier than neural networks. Another is that the code we downloaded was very difficult to understand due to a lack of comments and ambiguous variable names. We could determine where the shape contexts were computed, but not much more, and we did not have time to implement the algorithm from scratch.
Overall, we think we were successful. We implemented both neural networks and surpassed our initial goals for the project. It would have been nice to implement metric learning or shape contexts, but since we spent too much time determining what the right alpha values to use were and had difficulty working with the shape context code, we were unable to realize these secondary goals.
We believe neural networks perform handwritten character recognizition extraordinarily well, but they also have a few drawbacks. They take copious amounts of time to train and are difficult for humans to understand. It's easy to look at a decision tree and know what's going on, but you really have no idea what's happening in a neural network - they're too complex. Despite these drawbacks, neural networks and convolution networks seem to be the state of the art for tackling handwritten digit recognition.
[1] Y. LeCun, C. Cortes. 2000. The MNIST Database of Handwritten Digits.
[2] S. Roewis, Data for MATLAB hackers.
[3] Wikipedia. Intelligent Character Recognition.
[4] Wikipedia. Neural Network.
[5] C. Bishop. Pattern Recognition and Machine Learning, Chapter 5.
[6] S. Russell, P. Norvig. 2002. Artificial Intelligence : A Modern Approach. Second Edition. Sections 20.5 and 20.7
[7] B. Anguelov. April 3, 2008. Taking Initiative, Basic Neural Network Tutorial - Theory.
[8] B. Anguelov. April 3, 2008., Basic Neural Network Tutorial - C++ Implementation and Source Code.
[9] C. Stergiou, D. Siganos. Neural Networks.
[10] D. McAuley, S. Dennis. BrainWave 2.0, The BackPropagation Network : Learning By Example.
[11] I. Galkin. Crash Introduction to Artificial Neural Networks.
[12] Lisa Meeden, Derivation of Backpropagation.
[13] Wikipedia. Sigmoid Function.