Learning Bayesian network using EM algorithm from Incomplete Data

Problem Statement

We often encounter missing values or hidden variables in learning Bayesian networks(BNs) from medical data. However, most existing state of the art learning algorithms are not able to learn structure from incomplete data. Hence, I propose to use EM algorithm to learn BNs from incomplete data.

Methods

There are two major components for Bayesian Network learning:

● to Implement EM algorithm for parameters learning ,i.e. conditional probability table

● to learn structures using Bayesian Information Criterion (BIC)

Data

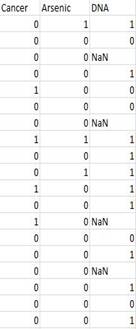
The data I used came from Dartmouth medical school. The table below shows a portion of the data I used for this analysis. This date set consists of 3 variables and 1113 observations. About 20% of values in DNA are missing. These three variables are arsenic exposure,Xrcc3 DNA genotype, bladder cancer. According to a recent study from Dartmouth Medical school, there is evidence of gene-environment interaction between XRCC3 variant genotype and high toenail arsenic levels on bladder cancer risk (Andrew 2009a).

Brief Introduction to Bayeisan Network

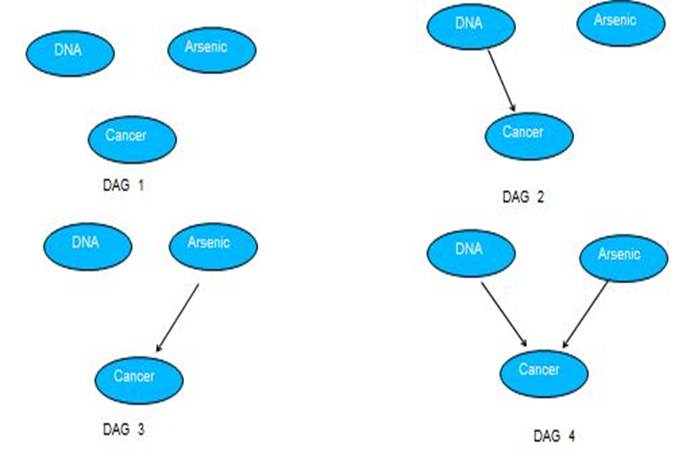
The Bayesian network below is a suggested one based on Dr. Andrew's study, which illustrates interactions among those three variables. In this DAG, arsenic exposure and DNA are found to influence cancer. There conditional probability tables associated with each node are also given.

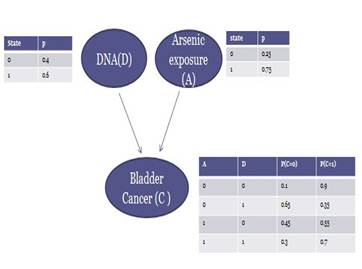
A typical BN consists a directed acyclic graph(DAG) and the conditional probability tables. The edges represent causal relationship between variables. For a particular BN, the joint probability of variables is shown in the following function:

Parameters learning from missing data

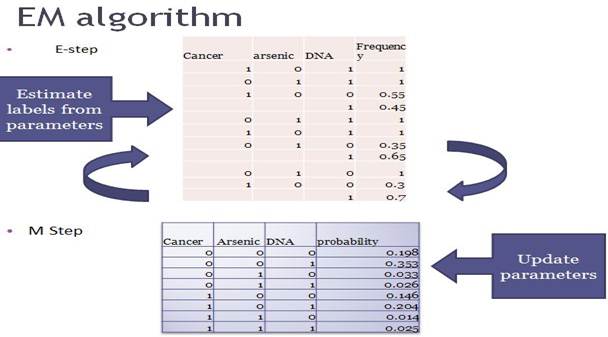
In the E-step, the algorithm estimates the labels of missing data from parameters. For each observation with missing values, the algorithm assign frequency to them based on the conditional probability tables. After each E-step, the date set are updated, from which we can future derives new parameters in the M step. The whole process repeats until it reaches convergence, i.e. when the log-likelihood of parameters stop changing. The log-likelihood of the entire data is shown in the function below:

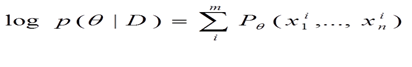
Structure Learning

Once parameters are learned, we can search through all possible structures. According to the prior knowledge, the relationship between DNA and Arsenic exposure are independent, hence only four possible structures or DAGs are listed below. The algorithm searches through the space and find the structure that optimally describe the data set based on penalized likelihood score, which is Bayesian information criterion(BIC) in this model . BIC score is described in the following function , while L is the maximized value of the likelihood function for the estimated model; k is the number of parameters; m is sample size. The structure with lowest BIC score is the optimal structure.

Results

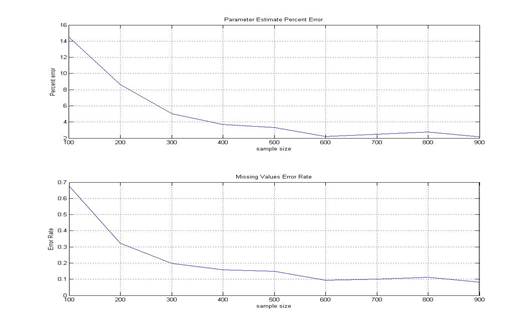
The EM algorithm estimates parameters more accurately as the sample size increases. From the percent error graph, percent error is close to 2.16% when the sample size is 900.

Percent error= Error rate for missing values also drops as sample size increases. When the sample size is 900 the error rate is 0.0812.

,

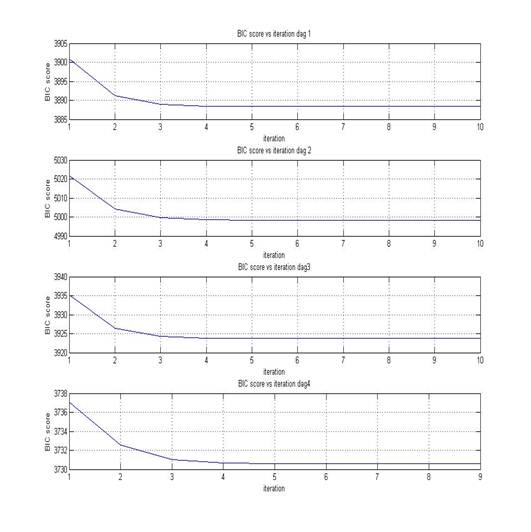
The graph below shows BIC scores versus EM iteration. We can see that DAG 4 has the lowest BIC score. Thus DAG 4 is the best model learned by the algorithm, which is consistent with structure proposed in the introduction

Conclusion

I have accomplished what I have proposed in the project proposal and the algorithm satisfactorily estimates parameters using EM method and the BN learned from this algorithm is consistent with the Dr. Andrew's study. However, the current model can only be applied to data with small size of variables. Besides, since we assume that there are no hidden variables apart from DNA, arsenic and cancer, the BN learned in this model might be different with the inclusion of other caner risk factors such as gender, ages and smoking. Future works would be to develop models that can handle more variables and more complicate BNs.

References:

Andrew, A.S., Mason, R.A., Kelsey, K.T., Schned, A.R., Marsit, C.J., Nelson, H.H., Karagas, M.R., DNA repair genotype interacts with arsenic exposure to increase bladder cancer risk. Toxicol. Lett., 187,10-14, 2009a.

Friedman, N. 1998. The Bayesian structural EM algorithm. In Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence (UAI-98), Cooper, G. F. & Moral, S. (eds). Morgan Kaufmann,129-138.

Darwiche,Adnan ., Modeling and Reasoning with Bayesian Networks. Cambridge University Press, 446 pp., Cambridge, UK, 2009.