Detection, Classification, and Recombination of Musical Style Motifs
Daniel Muldrew

Key Problem: identify important representative musical motifs present in different styles of music.

Secondary Problems: evaluate the application of musical motifs in classifying musical styles and as a basis for generating new music of a particular style.

Methods:

After my project proposal, I reviewed the literature further on motif detection algorithms. Evaluating their applicability to music changed my notion of what music motifs are, and how they are different from motifs found elsewhere. Unlike motifs in DNA, a satisfactory description of musical motifs cannot be limited to simple sequence matching of strings representing the notes. Motifs in music are often transformed by standard techniques such as transposition, ornamentation, and inversion [1].

Calculating a spectral ranking of segment similarity instead of segment repetition has resulted in better detection of important recurring sections of a musical piece [3]. Motif algorithms which rely on detecting a high repetition of a sequence of notes can lead to false positives, and do not easily detect the "varied repetition" of the motif. Ornamental trills are a good example of a highly repeating structure that is not a central theme to piece.

Spectral ranking measures the centrality of musical segments related by a notion of similarity computed using musically relevant metrics. Eigenvector centrality can also be seen as a weighted sum of not only direct connections, but also indirect connections of every length. Different metrics can be used and created to detect motif transformations beyond simple repetition.

Results:

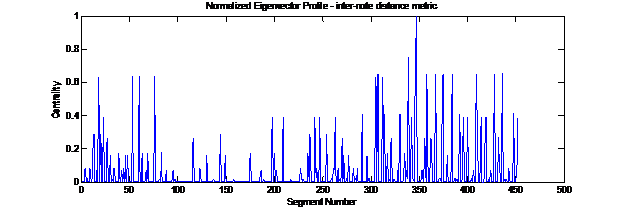
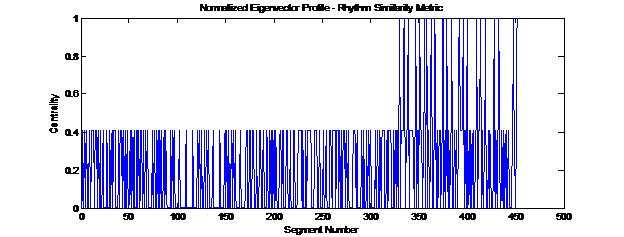
Below 30 songs of folk music were segmented in terms of single bars (or measures). Different metrics were used to identify similarity between the segment. What follows are the graphs of the normalized spectral ranking of all segments. Using a threshold on centrality, important segments in the genre are readily identified. The resulting segments where inspected to make sure that the similarity metric worked as intended.

Spectral ranking for a metric invariant to octave transposition from [3]:

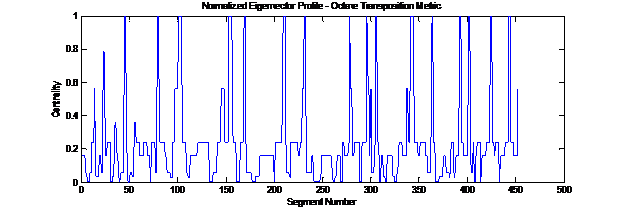
Spectral ranking for a inter-note distance metric invariant to arbitrary transposition from [3]:

Spectral ranking for a metric of rhythmic similarity which I devised:

What I would still like to do:

Test other potentially useful musical metrics, such as a "subset" metric that will detect motifs between simple segments and those with ornamentation.

Evaluate whether high-centrality motifs are a useful basis for a classifier of music style.

Even if this approach fails, such a result would still be interesting because it could indicate that musical motifs might transcend genres.

Finally if there is time, I would really like to use genetic algorithms to create new music using motifs as building blocks.

After an initial time investment to more completely review the motif detection literature and select a method, I'm close to my milestone goal of having a motif database for different styles which I can apply to at least one of my secondary problems.

References

1. http://core.ecu.edu/music/jacobse/classes/analysis/PHRASES.HTM

2. A. Pinto and Paolo Tagliolato, "A Generalized Graph-Spectral Approach to Melodic Modeling and Retrieval," MIR '08, Oct 30-31, 2008, Vancouver, BC, Canada.

3. A. Pinto, "Relational Motif Discovery via Graph Spectral Ranking," MLG'10, July 24-25, 2010, Washington DC, USA.

4. Can Yang, Chi K. Tse, and Xiaofan Liu, "Analyzing and Composing Music from Network Motifs" http://www.eie.polyu.edu.hk/~xfliu/publications/NOLTA09Motif.pdf

5. CK Tse, X Liu and M Small, "Analyzing and Composing Music with Complex Networks: Finding Structures in Bach's, Chopin's and Mozart's," International Symposium on Nonlinear Theory and Its Applications, Budapest, Hungary, pp. 5-8, September 2008.

6. X Liu, CK Tse and M Small, "Composing Music with Complex Networks," Workshop on Complexity Theory of Art and Music, International Conference on Complex Sciences: Theory and Applications, Shanghai, February 2009.

7. Sebastiano Vigna, "Spectral Ranking," 2011. http://arxiv.org/abs/0912.0238

8. Michael Towsey, Andrew Brown, Susan Wright, and Joachim Diederich, "Towards Melodic Extension Using Genetic Algorithms" Educational Technology & Society, 4(2), pp. 54-65.

9. M. Chan, J. Potter, and E. Schubert. Improving algorithmic music composition with machine learning. In Proceedings of the 9th International Conference of Music Perception and Cognition, Bologna, Italy. 2006.