
| Description | | | Progress | | | Tests | | | Results | | | Next Steps | | | Miscellaneous | | | References |
The problems of parsing music structure and artificially composing new music both require defining the simplest musical units, or features. In most cases, these simple features are derived from music theory: chords, syncopations, melodic intervals, etc.
Other fields of machine learning such as speech and image recognition all seem to reach the same conclusion: hand-coding low-level features in a recognition system introduces a strong bias. For example, many image recognition algorithms define the simplest features in terms of only edges (ignoring other known features such as center-difference contrast). An alternative is to have an algorithm process a some set of training images and learn a set of simple features from them. This approach generally results in better recognition. Many algorithms have been developed to this end [1–4].
My project is to implement the feature-learning algorithm described in this paper, and run it on samples of music instead of images. The goal is to see if the features learned have semantic meaning, and if classification done using these features performs better than using hand-coded features.
My milestone goal was to choose an implement an unsupervised-feature-learning-algorithm, and get preliminary results on Joplin songs. I'm slightly behind my goal in that I've run these tests but haven't had time to tune them or interpret results (turns out each test takes over 30 min to run).
Choice of Algorithm
At the time of the proposal, I hadn't decided on an algorithm yet. I wrote then that I would choose between Convolutional Sparse Coding (CSC), Invariant Predictive Sparse Decomposition (IPSD), and Shift Invariant-Probabilistic Latent Component Analysis (SIPLCA) [2, 3, 4]. All of these extend the basic idea of learning convolutional features in images in some way specific to images. For example, the selling point for Convolutional Sparse Coding is that it avoids redundancy between features that occur because lines in images tend to be continuous, so the set of features may have multiple representations of the same fundamental feature. I chose not to implement this because songs are much sparser images with few to no continuous features. IPSD and SIPLCA similarly address image-specific problems that I do not think would apply to music processing.
In other words, I wanted to avoid over-complicating the problem, so I did not implement an algorithm optimized for image processing.
I chose to implement an algorithm which I call Iterative Sparse Encoding (ISE) developed by Olshausen and Field because it is elegant, simple, and effective [1]. The algorithm works by minimizing a simple error function, E. Given a set of features (basis matrices), find the linear combination of them that best reconstruct a training image using as sparse weights as possible (i.e. most weights close to zero). E is defined as the reconstruction-error (how poorly the image is reconstructed) plus the denseness of the weights (opposite of sparseness). Minimizing E with respect to these two simple criteria produces a set of features that capture the dominant components of the image.
Harmony Boosting
Grayscale images have pixel values anywhere between 0 and 1. My representation of songs is a boolean matrix where an index is 1 if an only if that pitch is on at that beat. In this representation, a piano song is like a #beats X 88 boolean image. Song matrices are very sparse (even playing a note with every finger, you won't activate more than 11% of the notes on any beat). I'm not sure if this sparseness is a problem in terms of processing the song as an image.
Harmony Boosting is something I came up with to address this 'problem' of sparseness, and as a way of fixing the problem of intervals (where a 10th is similar to a 3rd). I define a set of weights to iteratively 'boost' values at certain intervals. It works as follows: Let w_octave be the boosting weight for octaves (0 ≤ w_octave ≤ 1) and N be some note (1 ≤ N ≤ 88). The notes octave away on either side (N ± 12) get value N * w_octave. After a second iteration, we see that N ± 24 (two octaves away) get w_octave^2. This both makes songs real-valued in [0, 1], and less sparse, without really changing the structure of the song. The weights for all intervals 1:12 as well as the number of boosting iterations to perform are hyper-parameters.
In the tests section, below, I discuss the different results when using harmony boosting or not. Briefly, the result is that using harmony boosting in learning or not makes no obvious visual difference in features, so I need to still test if it affects classification accuracy.
To verify that the ISE algorithm was working properly, I wrote a lot of test code with both contrived/simple tests and some more difficult ones. I can also use these tests to experiment with hyper-parameters.
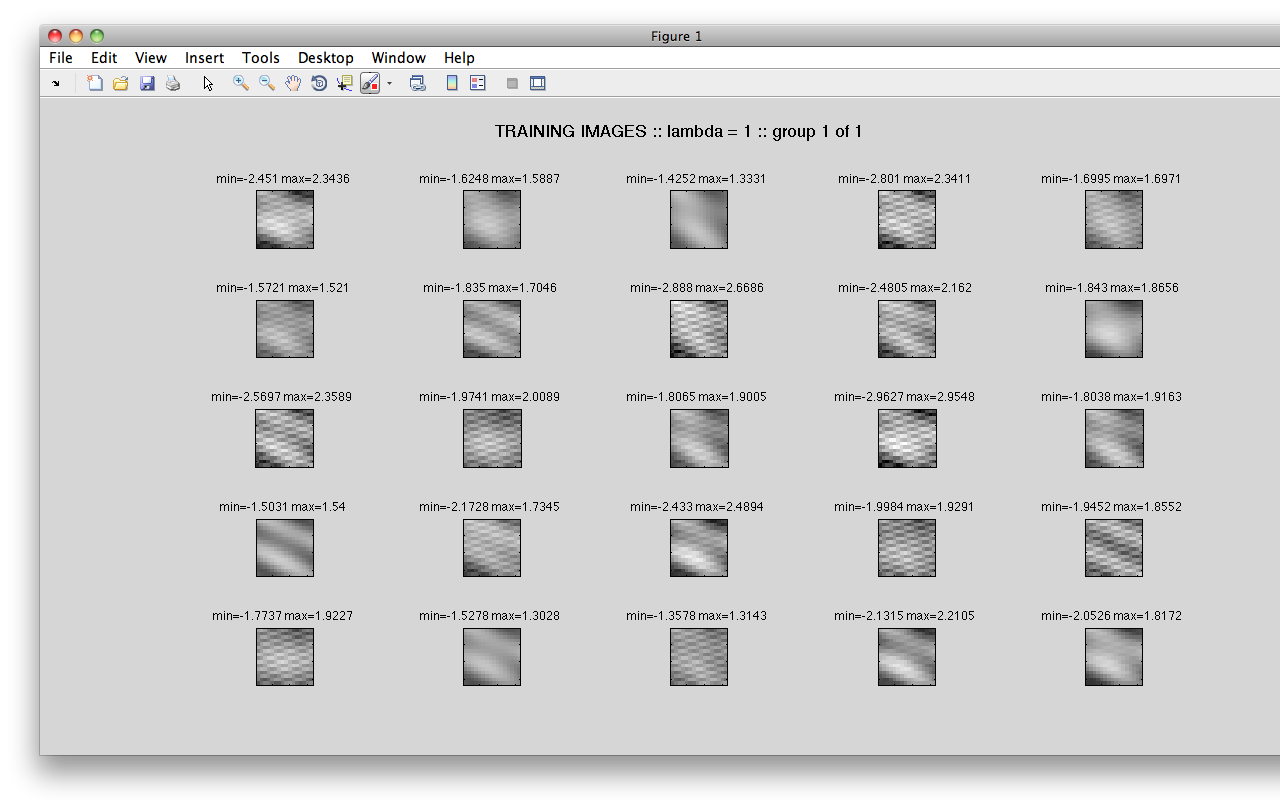
K: number of training imagesN: number of featuresDIM: each image (and feature) is DIM x DIML: number of iterationsK=4; N=3; DIM=4, L=500This test is a very simple demonstration of the algorithm and is a good quick-check that there are no bugs.
Training Set

Learned Features

Reconstructed Images

K=25; N=5; DIM=16, L=500This test was intended to show off how, if images are generated as a sum of features, ISE can recover those features. It didn't recover the features, but it still does impressive reconstruction. Maybe it sees something we don't..
Features used to construct training set

Learned Features
Training Images vs Reconstructed Images (mouseover to change)
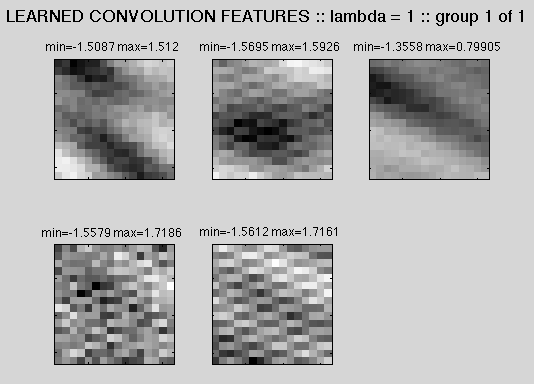
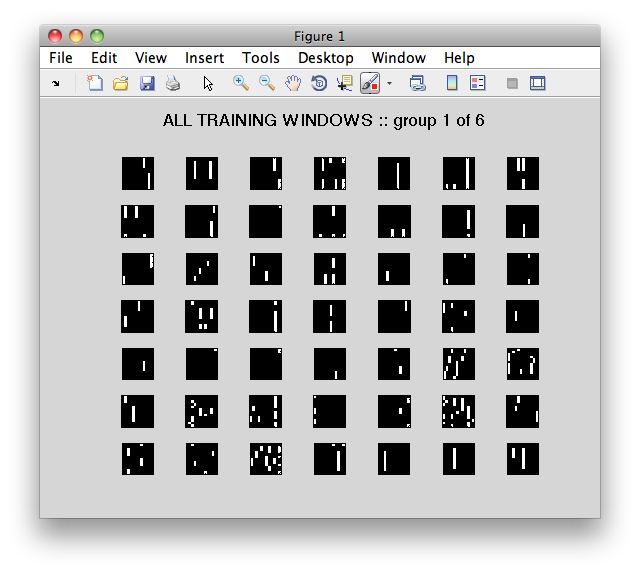
K=270; N=144; DIM=12, L=500I have 18 Scott Joplin songs' midi files. From each of these, I sampled 15 random nonzero chunks, each 12x12 (beats x pitch), resulting in 270 total training images. I trained 144 features to reconstruct them (in theory this could be one per pixel). Basically, the features can reconstruct the original windows well but basically look like static.
In the following images, the x-axis is pitch, the y-axis is beat. A vertical white line is one note held over many beats.
Learned Features (first 25 of the 144 - the rest are more of the same)

Training Images vs Reconstructed Images (first 49 of each. Mouseover to change)
K=270; N=144; DIM=12, L=500I managed to misplace the images for this test, and it takes a long time to re-run (more time than I have), but the results were almost identical to test #3: static-y features but good reconstruction
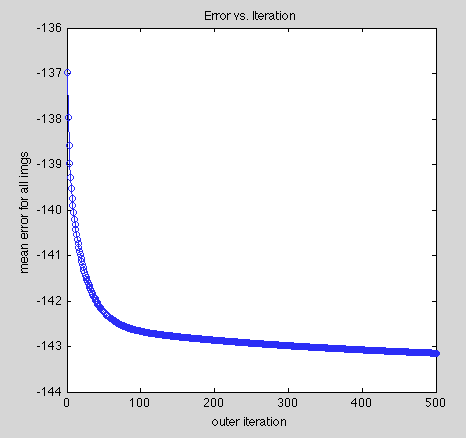
The error function defined in [1] is easy to compute, so I just made this graph to verify that I was, in fact, minimizing the error over iterations. It was easy to be skeptical after those static features..
The results of the grating test were that the training images could be reconstructed well with a set of features that don't match the features used to generate the images. This could be good or bad. On the bright side, the algorithm is open-minded to learning its own set of features. On the other hand, I was hoping to find simple structures in the images, and I'm not getting those yet. I need to do further testing with the hyper-parameter lambda (from [1]) - I'm guessing that changing lambda (prioritizing reconstruction or sparseness) will control where the features fall on the static–structure spectrum. Similarly, maybe just running out to more iterations, more or fewer features, etc. could all affect the quality of the features.
The tests done on songs have the same problem; reconstruction is accurate but the features are meaningless. I'm hoping that fixing this for the gratings will also fix it for songs.
I have a few more tests to run (mentioned above) to experiment with hyper-parameters before diving deeper into music-learning. Assuming I can start to get 'structured' features out of the ISE algorithm, I will compare them to theory-based features, such as those outlined in a paper by Michael Towsey [5].
Very soon I need to find an algorithm that does classification based on convolutional features, and test my different feature sets. Here are some tests I plan to do once I have a classifying algorithm: