Collaborative Filtering Algorithm Applied to MovieLens Data
Introduction
The goal up to the milestone deadline was to implement incremental singular value decomposition. This goal was met and variants of it were implemented. Another different method used in Netflix prize called Restricted Boltzmann Machine was attempted. This was less successful and it's unfortunately very difficult to make sense of the different parameters that need to be optimized.
Methods
Two main methods were implemented in Matlab both of which are based on the latent factor models:
- Incremental Singular Value Decomposition (Incremental SVD)
The two main problems with pure SVD applied to huge sparse matrix are:
- Original SVD is not defined for a matrix which is mainly sparse,
- Computing SVD i.e. A = U Σ VT is prohibitively expensive, where the different matrices have their usual meanings
The version that has been implemented in Matlab is the one that was ranked high in Netflix prize 2007 [3] and variants of which have subsequently been used in Netflix prizes [2].
It uses gradient descent to minimize the Frobenius norm between the user-movie matrix, A and an approximation of it, Aapprox = U * MT where the qth row of U represents the preference of user q and the wth row of M represents the movie, w feature vector.
Regularization was also added to decrease the error of the predicted ratings on the testing datasets but this parameter was not optiized through cross validation because of the time it takes to run the algorithm.
In [7], the authors describe a way to decompose the ratings into biases. The idea is that some users might have a tendency to give higher rating. So, in this case the biases on item and user are added and learnt using gradient descent.
- Restricted Boltzmann Machine (RBM)
Restricted Boltzmann Machine (RBM) is a two layer bipartite graph i.e. it consists of one layer of hidden units (h) and another layer of visible units (v) all interconnected except in the same layer. Each connection would have a weight associated with it and the aim is to learn those weights and biases associated with the hidden and visible units.
RBM was applied to collaborative filtering by the authors of [1]. Movies are denoted by 1 and the ratings are divided in K discrete values which would make up the set of visible units of dimension K by M [1]. Each user would have his own RBM. A missing rating is simply not accounted for in the visible unit. To summarize each user has his own RBM, the number of hidden units is specified by the programmer, the number of rows in the visible units remain fix with K different units (called softmax) and the number of columns i.e. number of movies would vary depending on the whether that movie was rated by the user under consideration. Given that we have v visible units and vik denotes the index into the visible units i.e. if a user, u has rated movie i with a rating k the vik would be one. To make the algorithm run faster Contrastive Divergence was also implemented. The idea here is to update the visible and hidden units alternately for some specified number of steps.
Testing
The movielens data set was used. It consists of 80000 ratings in the training sets and 20000 ratings in the testing set. The matrix is a 943 (users) by 1682 (movies). The root mean square error (RMSE) was computed between the observed ratings in the testing set.
Results
The root mean square errors of the test ratings were computed for each method and Table 1 summarizes the results. The RMSE are worst than expected because no optimization was performed.
| Algorithms | RMSE |
| Incremental SVD | 0.938 |
| Incremental SVD with Regularization | 0.964 |
| Incremental SVD with Regularization with Bias | 0.991 |
| Restricted Boltzmann Machine | ~3? |
Figure 1 shows the decrease in RMSE as the number of iterations is increased (for the case of incremental SVD).
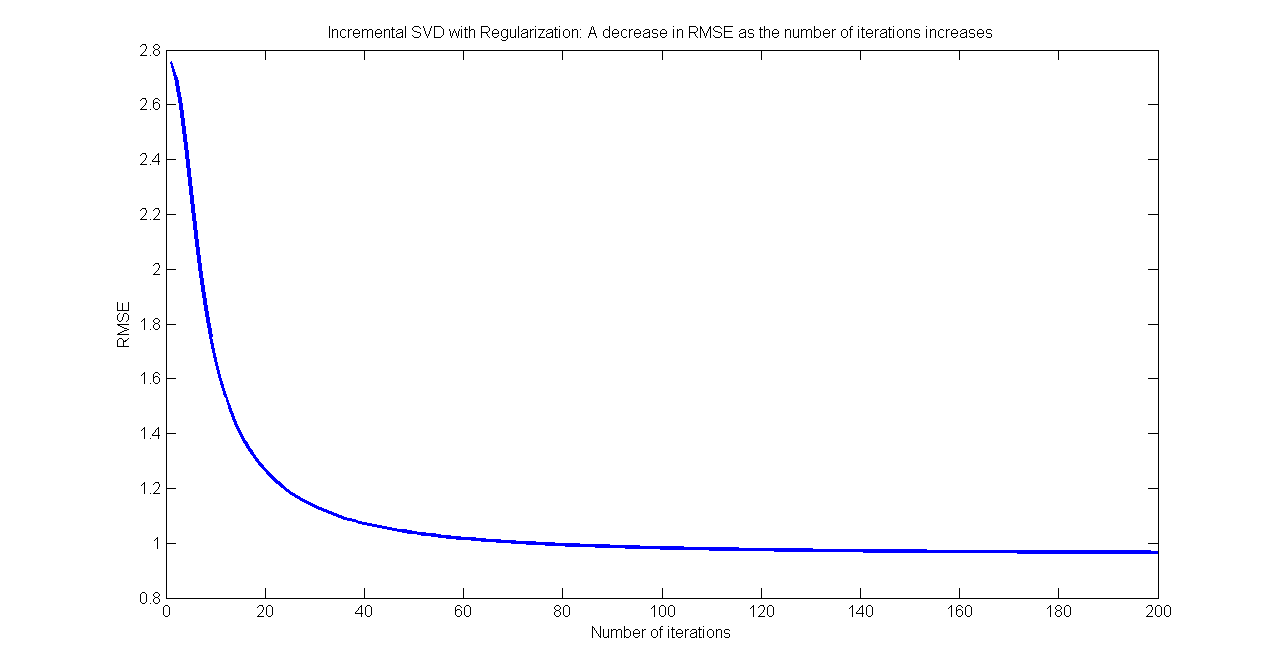 Figure 1: Variation of RMSE as the number of iterations increases
Figure 1: Variation of RMSE as the number of iterations increases
Problems
Except for the running time to compute the rmse, incremental singular value decomposition did not cause much trouble. RBM, on the other hand, did cause some difficulties since, knowledge on the actual network was not enough, Gibbs sampling and Contrastive Divergence were also implemented but in the end the number of parameters (hidden units, biases for the visible and hidden units, momentum, weights, regularizations for each and more ) that have to be controlled and the time it takes to do each iteration caused very poor optimization resulting in very bad rmse.
Conclusions
The main goal of this project has been achieved whereby the results of incremental SVD have indeed showed that it's a good model for predicting the ratings of users. Implementation of RBM, on the other hand, which wasn't the main focus of this project was not very successful.
References
[1] Restricted Boltzmann Machines for Collaborative Filtering, Ruslan Salakhutdinov, Andriy Mnih, Geoffrey Hinton, International Conference on Machine Learning, Corvallis, 2007
[2] The BigChaos Solution to the Netflix Grand Prize, Andreas Toscher, Michael Jahrer, Robert M. Bell, 2009
[3] http://sifter.org/~simon/journal/20061211.html
[4] http://www.cs.toronto.edu/~hinton/csc2515/notes/pmf_tutorial.pdf
[5] http://www.grouplens.org/node/73
[6] Clustering Items for Collaborative Filtering Mark O'Connor & Jon Herlocker, ACM SIGIR Workshop, 1999
[7] Improving regularized Singular Value Decomposition for collabora- tive filtering. Proceedings of KDD Cup and Workshop, A. Paterek