Learning Bayesian network using EM algorithm from Incomplete Data

Recap of Problem Statement and Progress

We often encounter missing values or hidden variables in learning Bayesian networks from medical data. A BN usually consists of a directed acyclic graph (DAG) and conditional probability distributions associated with each node in the DAG. The conditional probability distributions are the parameters we are learning and usually they can be learned from a fixed DAG. Hence the first task of the project is to develop codes for learning parameters from a fixed DAG. Once parameters are known, we can learn the structure by comparing different DAGs and choosing the highest scoring DAG. The scoring function used in this project is based on the likelihood function of parameters. I have finished the majority parts of developing codes for parameters learning and will start soon with structure learning.

Data

The data set consists of 3 variables and 1113 observations. These three variables are arsenic exposure, Xrcc3 DNA genotype, bladder cancer. According to a recent from Dartmouth Medical school(DMS), there is evidence of gene-environment interaction between the XRCC3 variant genotype and high toenail arsenic levels on bladder cancer risk (Andrew 2009). In this project, I use medical data obtained from DMS to investigate 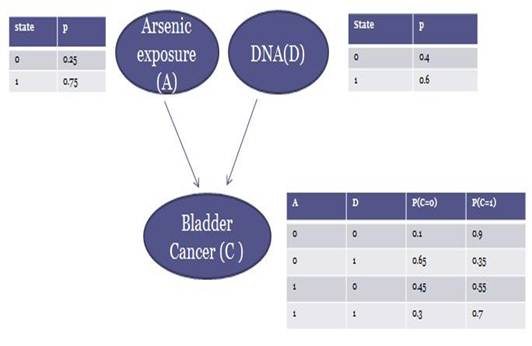$Description: Description: C:\Users\d41249s\Desktop\Capture.JPG$ interactions among genes, environment and cancer.

Method: EM algorithm in learning parameters

The Bayesian network on the right illustrates interactions among those three variables. In this DAG, arsenic exposure and DNA are found to influence cancer. Three conditional probability tables associated with each node are also given.

Say that we have 10 random observations. In which cancer and arsenic data are complete, while in obseravation2, 4, 5, 7 DNA values are missing. Note that the probability distributions given in the examples are for demonstration only and they are not real distributions.

Figure 1. A Bayesian Network

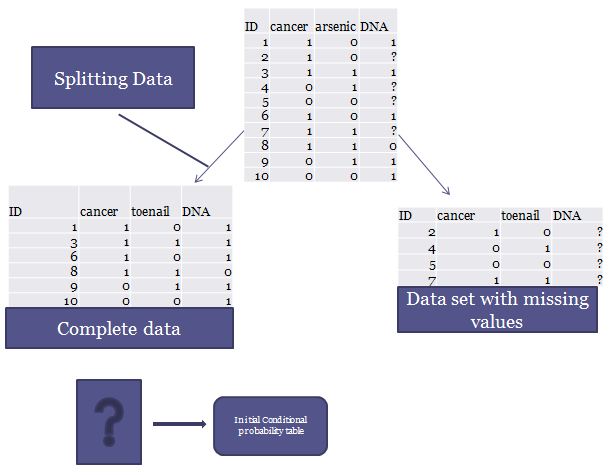
To begin with, I first split the original data set into two separate sets. One contains missing values; the other contains complete data. From the complete data set, I can generate initial conditional probability tables shown in figure 1. The whole process of splitting data is illustrated in Figure 2.

Figure 2. Initial Data preprocessing

$Description: Description: C:\Users\d41249s\Desktop\Capture1.JPG$

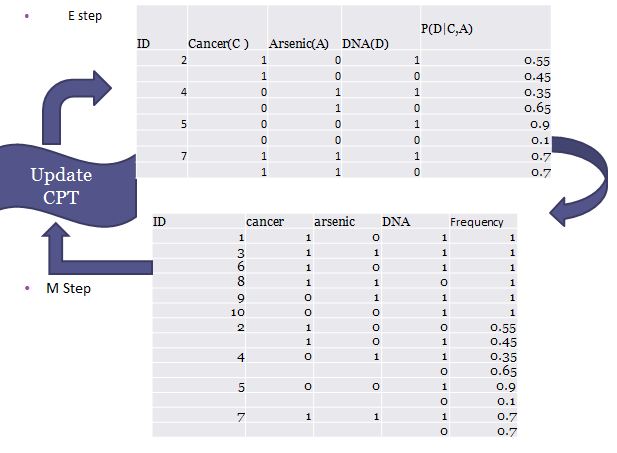
In the E-step, the expected conditional probability P (D|C, A) can be derived from the complete data set and so for each observation with missing value we can have two scenario for DNA equal to 1 and 0. In the current example, the four observations with missing values can be converted into 8 weighted observations with complete data. In the M-step, the new 8 weighted completed observations are then combined with the other complete data to calculate the new parameter and update the conditional probability table. This process is explained in figure 3. The whole process loops until convergence is reached, i.e. when the log-likelihood function of data given parameters remain unchanged.

The log-likelihood of data given the parameters is defined as the following function.

$Description: Description: C:\Users\d41249s\Desktop\Capture3.JPG$

Figure 3. EM process

$Description: Description: C:\Users\d41249s\Desktop\Capture2.JPG$

Since I have only three variables, I can generate all the possible DAGs for these three variables and compute the parameters and apply scoring function to find the most the structure that has optimal performance. So I will use approaches different from what is suggested in SEM, but still learn structures from missing values.

Future Works

Upon completion of developing codes for parameters learning, I will further develop codes for DAGs generation and scoring function to selects DAGs that best describe the data in the following three weeks.

Time Line for the following three weeks

Week 1: develop codes for DAGs and scoring function
Week 2: test codes and tune codes
Week 3: Final write-up and presentation

Reference

Andrew, A.S., Mason, R.A., Kelsey, K.T., Schned, A.R., Marsit, C.J., Nelson, H.H., Karagas, M.R., DNA repair genotype

interacts with arsenic exposure to increase bladder cancer risk. Toxicol. Lett., 187,10-14, 2009a.

Karagas, M.R., Tosteson, T.D., Blum, J., Morris, J.S., Baron, J.A. and Klaue, B., Design of an epidemiologic study

of drinking water arsenic exposure and skin and bladder cancer risk in a U.S. population. Environ. Health

Perspect., 106(Suppl 4), 1047-1050, 1998.

Karagas, M.R., Tosteson, T.D., Morris, J.S., Demidenko, E., Mott, L.A., Heaney, J. and Schned, A., Incidence of

transitional cell carcinoma of the bladder and arsenic exposure in New Hampshire. Cancer Causes Control,

15, 465-472, 2004.

Friedman, N. 1998. The Bayesian structural EM algorithm. In Proceedings of the Fourteenth Conference on

Uncertainty in Artificial Intelligence (UAI-98), Cooper, G. F. & Moral, S. (eds). Morgan Kaufmann,129-138.

Guo, Y.-Y., Wong, M.-L. & Cai, Z.-H. 2006. A novel hybrid evolutionary algorithm for learning Bayesian networks

from incomplete data. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2006),916-923.