- Introduction
|
- The field of Music Information Retrieval (MIR) is a broad
field in which researchers aim to learn about music, such as the
structure of a piece, how various pieces compare to each other, and how
to recommend music to listeners. There are both many tasks and
approaches in MIR, and one song can be represented in several different
ways.
- In our project, we are creating an algorithm
that detects structure in a musical song. By structure, we do not
necessarily mean verse or chorus. Instead, our algorithm should detect
the same kinds of structure that a human eye sees when looking at
a matrix from our dataset.
|
- Dataset
|
- We plan to use a
subset of the Beatles Dataset created by Prof. Michael Casey of the
Department of Music at Dartmouth College. Each song is represented by a
distance matrix of the squared-Euclidean distances between the
song’s audio shingles. The audio shingles are comprised of 30
feature vectors, which are created by splitting the audio track into
tenth of a second windows and extracting the mel-frequency cepstral
coefficients (MFCCs) for each of the windows. [1]
-
The following is a visualization of one song from the Beatles Dataset
that has been processed to separate recorded zeros from non-recorded
distances.
|
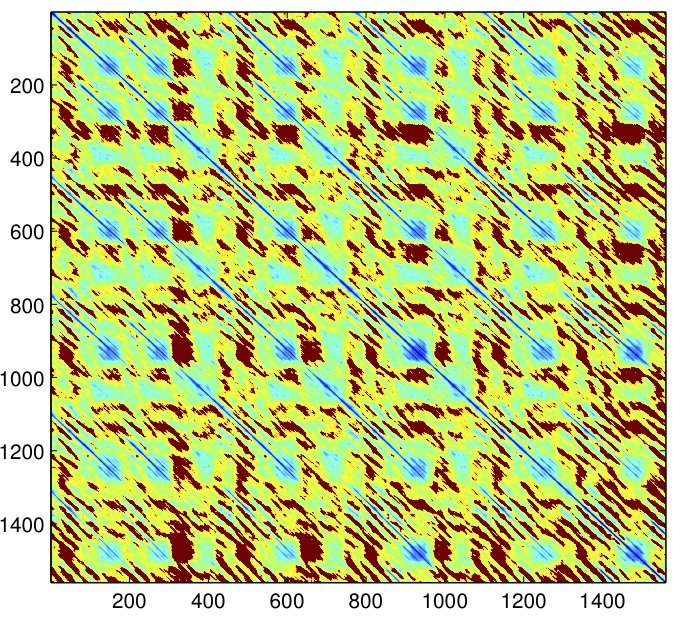 |
- Method
|
- The first phase of our
algorithm will be to identify and extract suitable feature vectors. For
our data, it has been observed that repeats in songs present themselves
as diagonals. [2]
Therefore instead of comparing whole sub-square-matrices, we will use
just the diagonals of sub-square-matrices. Another decision that we
will need to make is whether we will allow comparison of diagonals
whose sub-square-matrices overlap in someway.
- In the learning phase
of our algorithm, we will use unsupervised techniques such as spectral
clustering or k-Nearest Neighbor clustering. To objectively observe if
our algorithm is working, we will compare the results of the algorithm
to repeats found by a human coder.
|
- Timeline
|
- April 17:
Identify appropriate features from the square Euclidean distance
matrices
-
Begin
extracting features
-
Complete algorithm outline
- April 24:
Hand coding of training set complete; Feature extraction complete
- May 1:
Algorithm running; Begin processing on training set
- May 8
– Milestone:
Begin comparison and edit algorithm as needed
|
- References
|
- M. Casey, C. Rhodes,
and M. Slaney, Analysis of minimum
distances in high-dimensional musical spaces,
IEEE Transactions on Audio, Speech, and Language Processing 16
(2008), no. 5, 1015 – 1028.
- M. Müller, P,
Grosche, N. Jiang, A Segment-based
fitness
measure for capturing repetitive structures of music recordings, 12th
International Society for Music Information Retrieval Conference (ISMIR
2011), Miami, Oct, 2012.
|
