Structural EM Algorithm for Learning Bayesian Networks from Incomplete Data

A Bayesian network (BN) is a directed acyclic graph (DAG) in which nodes represent random variables and arrows represent

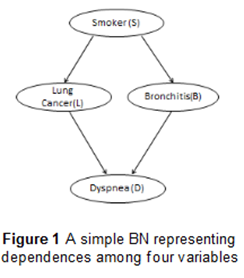
probabilistic dependencies between them. Figure 1 shows simple BN representing dependences among four variables.

There is an edge from S to L because Smoking has a direct influence on the presence of Lung Cancer. Smoking also

has a direct influence on the occurrence of Bronchitis. Dyspnea (shortness-of-breath) may be due to Lung cancer or

Bronchitis or both of them. BNs can be effective tools for combining prior knowledge with observational data

to infer model causal relations. Many existing learning algorithm can recover BNs from complete data. However,

we often encounter missing values or hidden variables in learning BNs in real-life application. People may simply

discard the missing values or replace them with certain values. Either of these approaches may lead to distorted BNs.

In this project, structural Expectation-Maximization (SEM) (Friedman, 1998) will be implemented to learn BNs from

incomplete data.

Friedman presented a structural EM algorithm for learning Bayesian network structures in the presence of missing values

and hidden variables in 1998. The search over the space of Bayesian networks alternates between two steps: an

optimization for the Bayesian network parameters conducted by the EM algorithm, and the structural search for a

better Bayesian network structure using the hill climbing strategy. At each step, it can either find better

parameters for the current structure, or selected a new structure. The former case is a standard "parametric"

EM step, while the latter is a standard "parametric" EM step.

I have available a rich genetic epidemiological data set from a large, population-based, case-control study of bladder

cancer in New Hampshire. These data include over 1477 SNPs in cancer-related genes, detailed smoking assessment,

gender, age, as well as other risk factors including arsenic exposure. (Karagas et,al, 1998, Karagas et al. 2004).

1. Implement EM algorithm to learn parameters 04/10-04/24

2. Implement Hill climbing to learn BNs 04/25-05/10

3. Write up milestone report 05-06-05-07

4. Testing and polishing results 05/11-05/20

5. Write up final report 05/20-05/25

Reference

Karagas, M.R., Tosteson, T.D., Blum, J., Morris, J.S., Baron, J.A. and Klaue, B., Design of an epidemiologic study

of drinking water arsenic exposure and skin and bladder cancer risk in a U.S. population. Environ. Health

Perspect., 106(Suppl 4), 1047-1050, 1998.

Karagas, M.R., Tosteson, T.D., Morris, J.S., Demidenko, E., Mott, L.A., Heaney, J. and Schned, A., Incidence of

transitional cell carcinoma of the bladder and arsenic exposure in New Hampshire. Cancer Causes Control,

15, 465-472, 2004.

Friedman, N. 1998. The Bayesian structural EM algorithm. In Proceedings of the Fourteenth Conference on

Uncertainty in Artificial Intelligence (UAI-98), Cooper, G. F. & Moral, S. (eds). Morgan Kaufmann,129-138.

Guo, Y.-Y., Wong, M.-L. & Cai, Z.-H. 2006. A novel hybrid evolutionary algorithm for learning Bayesian networks

from incomplete data. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2006),916-923.