Problem and Objectives

Our objective is to create a model to make predictions on two types of NBA bets: Over/Under (OU), which represents the combination of two teams' scores and Against the Spread (ATS), which represents the difference between two teams scores. To realistically make a profit in the betting system, our model must make correct predictions for 52.63% of the outcomes, our objective for the milestone was to achieve this level of accuracy.

We are assessing the performance of our model by computing its proportion of winning past bets relative to the cutoffs established by the bookmaker. We are also evaluating the performance of our models based on the root mean squared error of the raw numerical scores produced (i.e. sum and difference of point values).

Data

We are using two datasets for this project. One is collected from the ESPN database and contains all of the statistics (Shooting Percentage, Rebounds, Points, etc.) from ~2600 individual NBA games. Data from the 2009-2010 season will be used for training (754 samples) while 2010-2011 season data will serve for the testing purposes (811 samples). The second dataset is gathered from Oddsshark betting database, and contains scores of the games as well as ATS & OU odds given by the bookmakers for the individual games. [6] [7]

Methods and Results

Ensembles of Trees

Base Classifier: Pruned Variable Random Tree

We are using the VR-Tree as a base classifier for several ensemble methods composed of many individual trees. The VR-Tree algorithm works in a similar way as a regular decision tree except that there is a randomization factor introduced in the process of building a tree. As one of the parameters user must specify the probability with which tree will generate deterministic nodes. Randomly split nodes will be generated with the complement of the probability specified in the parameters. [3] [1]

Pruning is done based on reduced-error algorithm. While building each tree, 20% of the data is left out for the testing purposes. At each iteration the node that produces the biggest reduction of the error in test sample is selected for pruning. Iterations continue until further pruning becomes harmful. [1] [9]

Bagging

Bagging (Bootstrap sampling) relies on the fact that combination of many independent base learners will significantly decrease the error. Therefore we want to produce as many independent base learners as possible. Each base learner (VR-Tree in our case) will be generated by sampling the original data set with replacement. With each sampling there will be approximately 36.8% samples that have not been used for the training process. These samples will be used to estimate the error in pruning. N (user specified parameter) such ensembles will be generated and for each prediction each of them will vote. Average of their votes will be used as a final prediction. [2] [3]

Combination (OU) Bet:

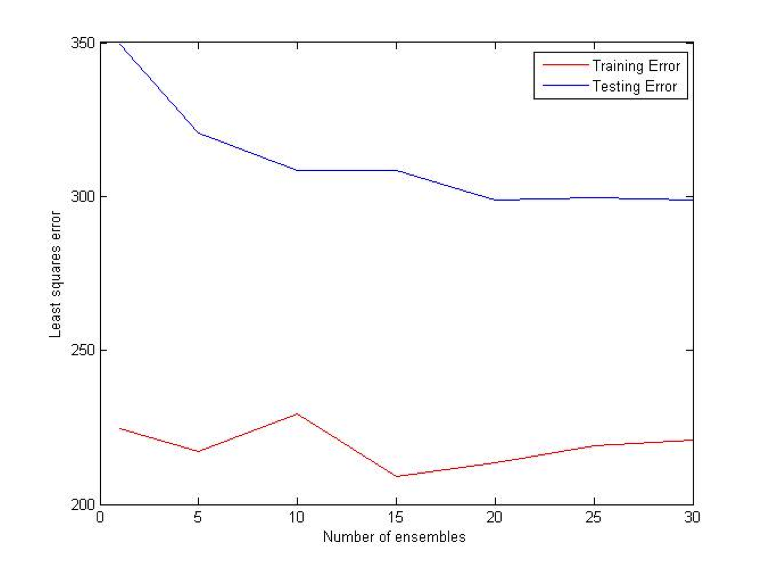
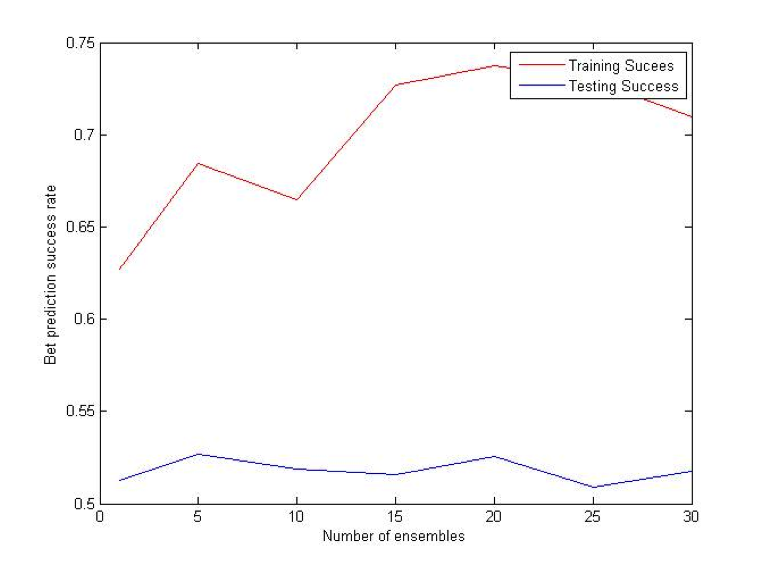
Difference (ATS) Bet:

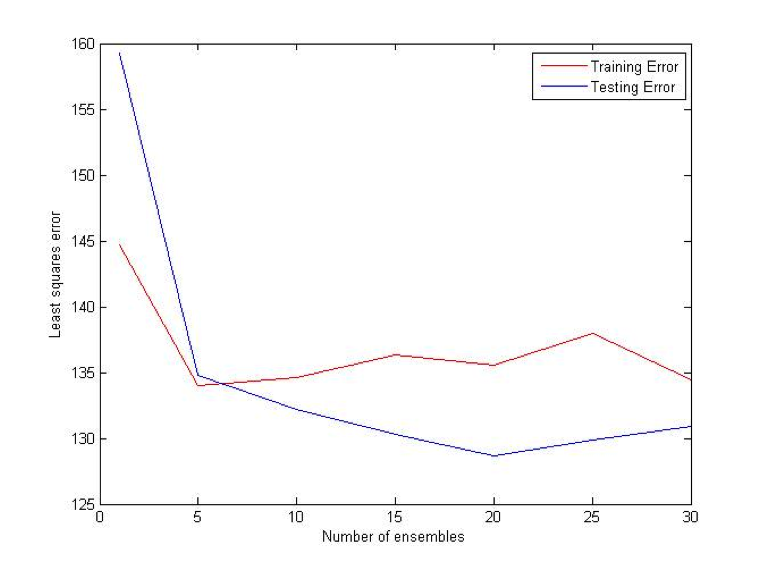
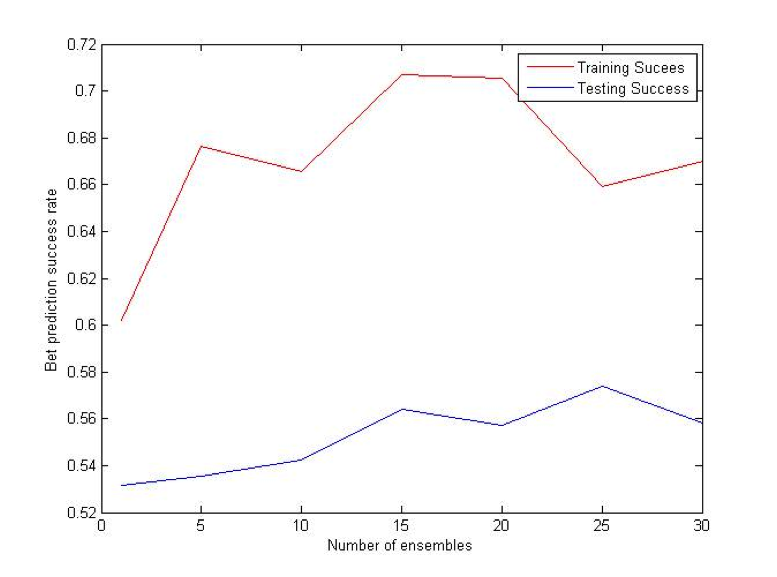
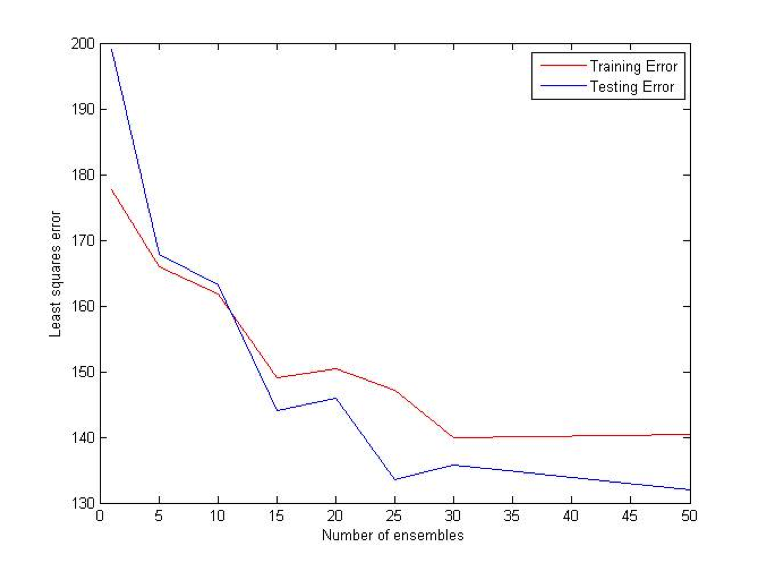
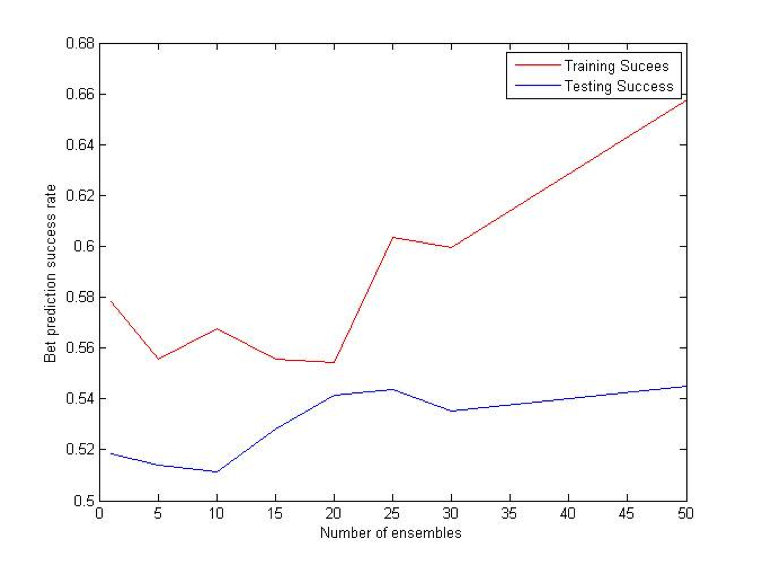
Coalescence

Coalescence is another ensemble method that relies heavily on randomly generated trees. N individual VR-Trees will be generated and each of them will have a different probability of producing deterministic nodes. As in the case with bagging, average of all N classifiers votes will be used for a final prediction. [2] [3]

Combination (OU) Bet:

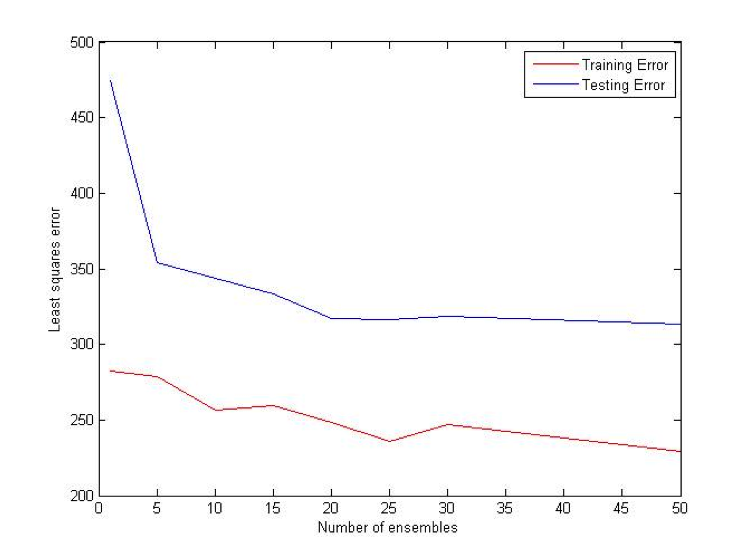
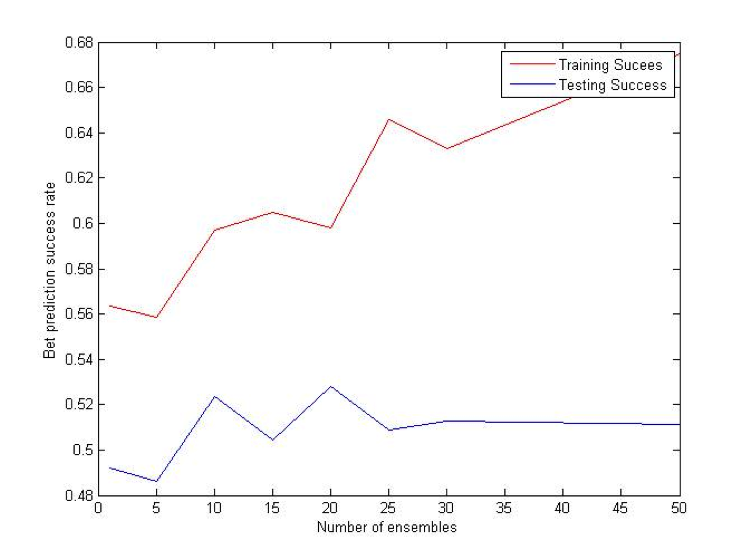
Difference (ATS) Bet:

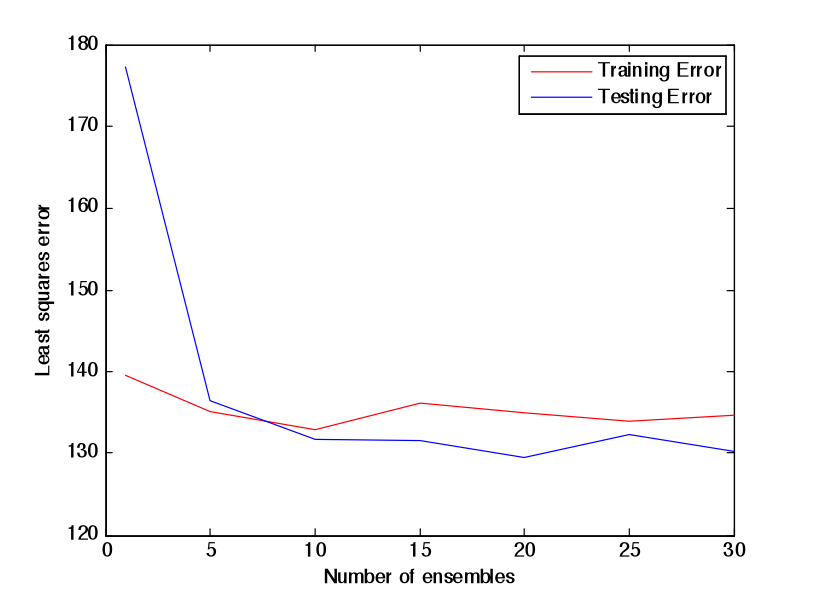
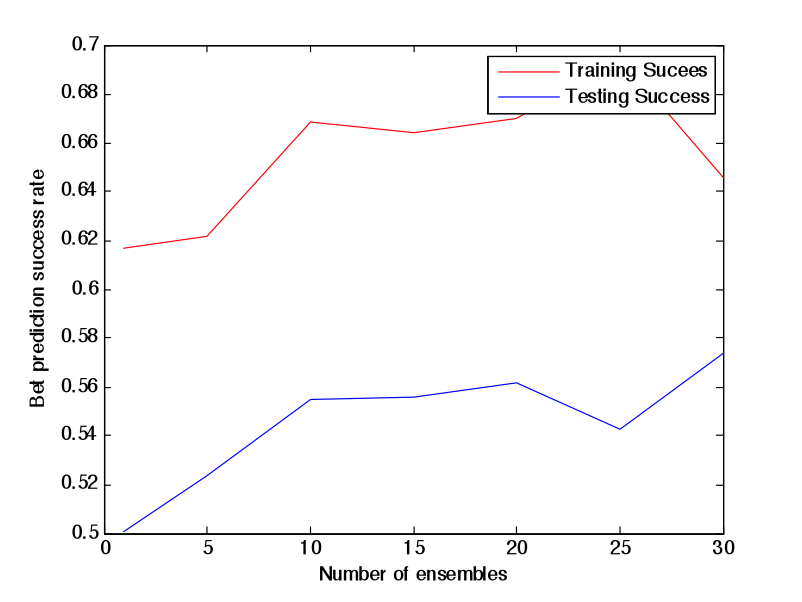
Random Forest

Random Forest is an extension of bagging where the major difference is the incorporation of randomized feature selection. At each step Random Forest algorithm will randomly select some set of features (subset of the original set of features) and produce a traditional deterministic split. N such trees will be produced, and their average vote will be used as a final prediction. [2] [3]

Combination (OU) Bet:

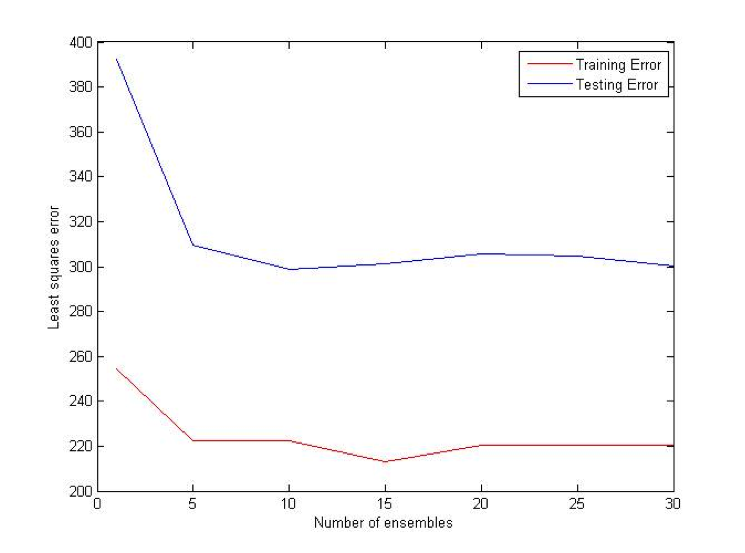
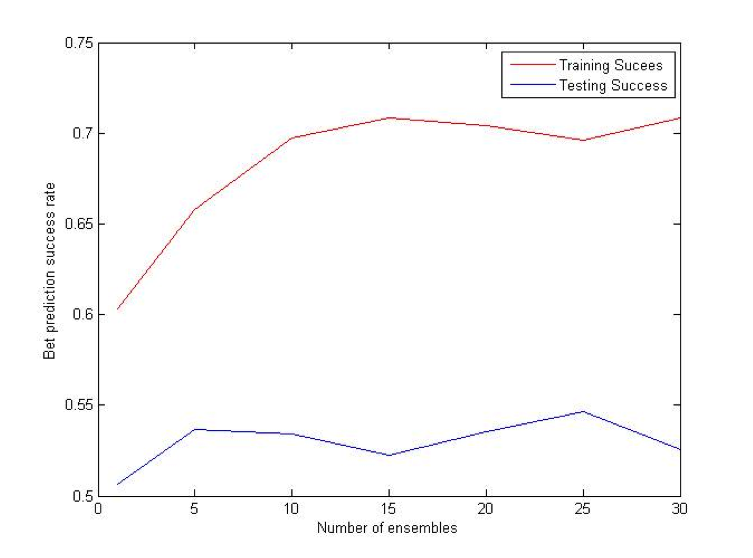
Difference (ATS) Bet:

Random Projections

Random Projections algorithm is almost identical to regular decision trees algorithms, except for the fact that it uses multiple features to determine the split at each node. At each split some subset of features is randomly selected. Then random weights for each of those features are selected. Finally, the best split for that particular set of weights is found. The procedure is repeated k times and the best resulting split is picked out of those k trials.

Combination (OU) Bet:

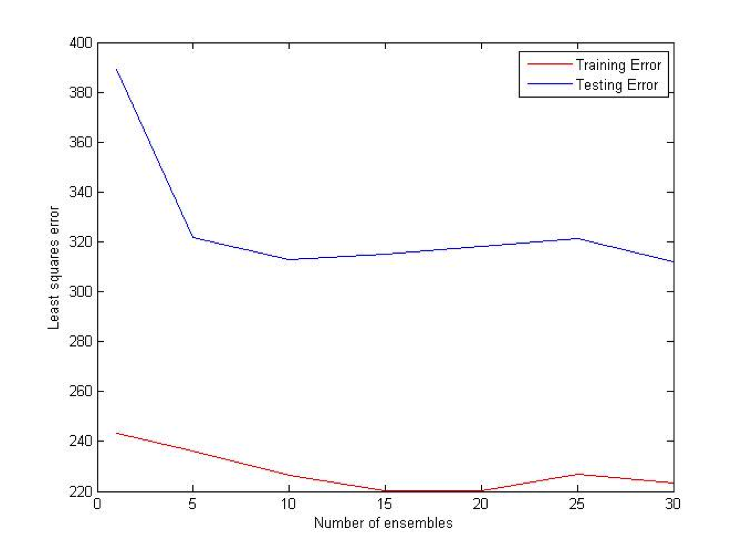
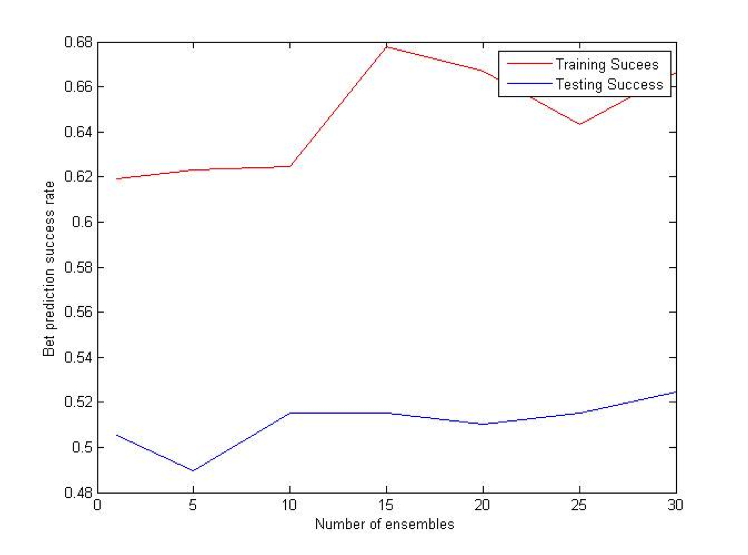
Difference (ATS) Bet:

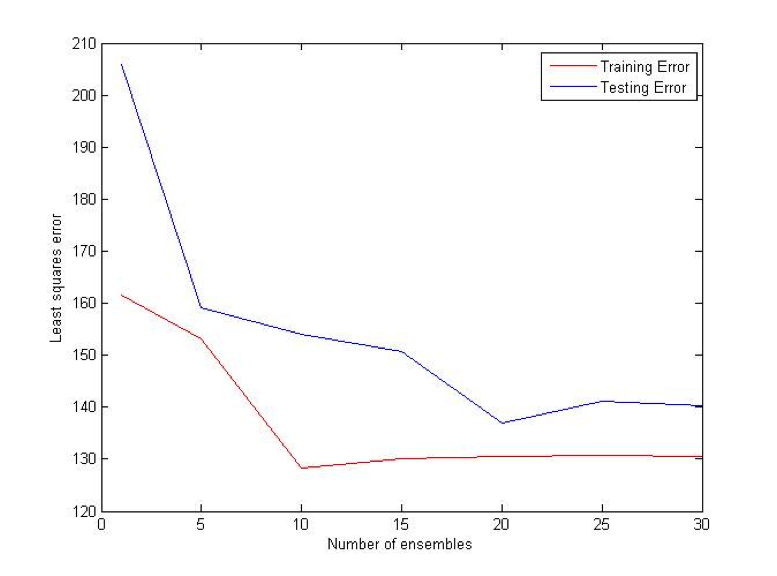
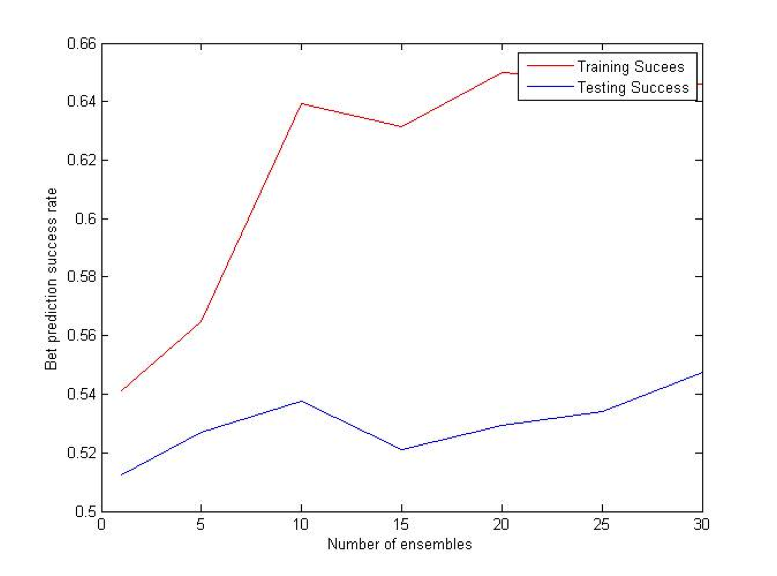
MultiBoost

MultiBoost algorithm combines two commonly used techniques: Bagging and Boosting. The motivation for MultiBoost algorithm comes from the observations that Boosting decreases bias of the error, while bagging decreases variance. Hence, combining two of these techniques may decrease both and increase the overall performance of the algorithm. Based on the empirical evidence, researchers claim that Adaboost gains the most benefit out of the first several iterations. As a result, it may be beneficial to let Adaboost run for some pre specified number of iterations, reset the weights, and then run it again. This procedure would be repeated until some termination criteria is reached. For this algorithm, we use VR-trees as our base classifier. [10]

Combination (OU) Bet:

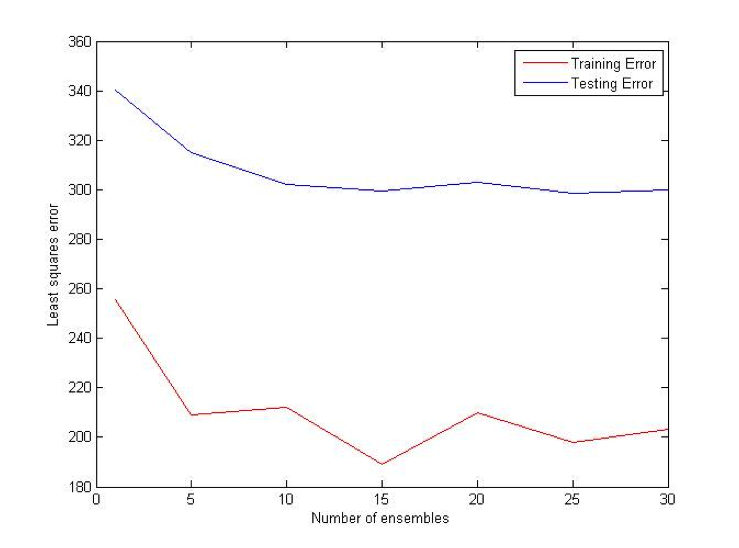
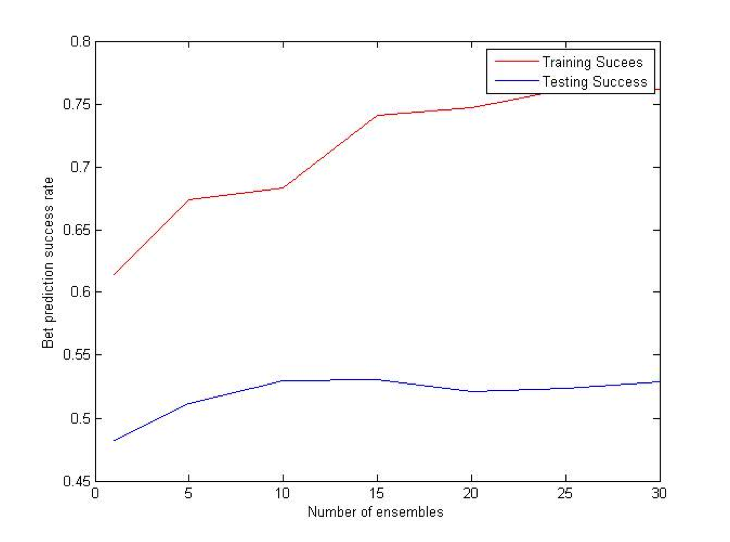
Difference (ATS) Bet:

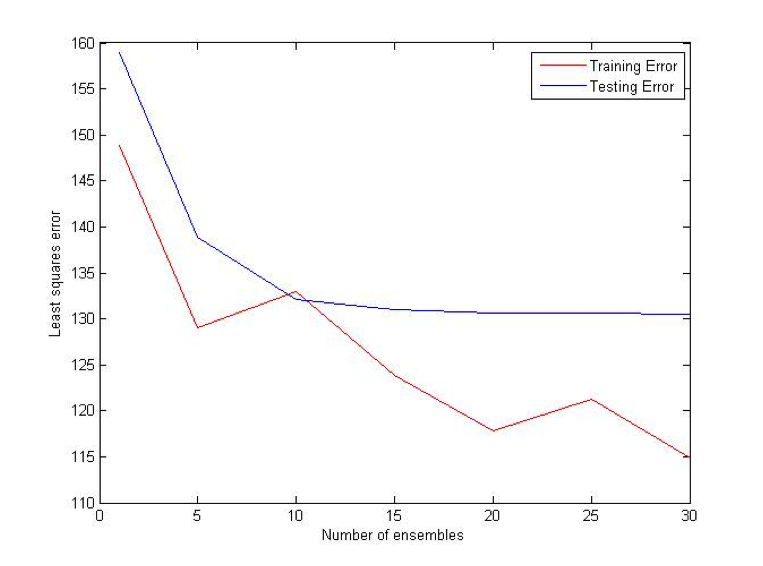
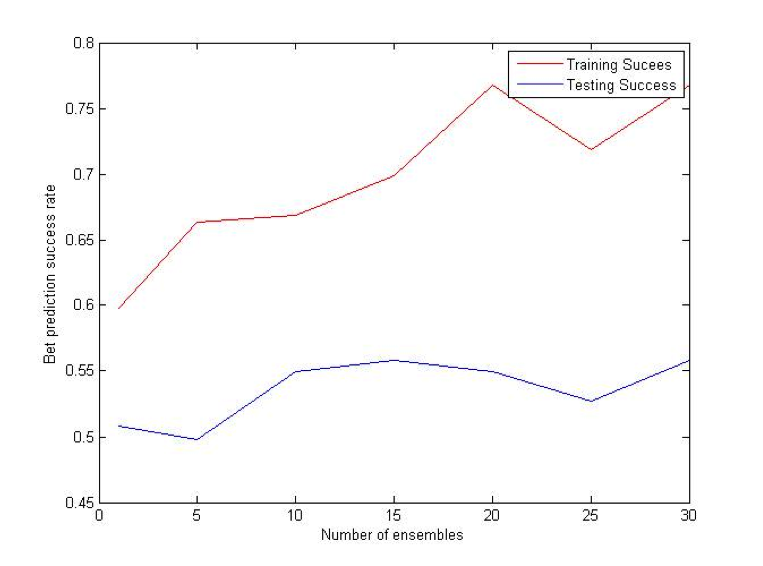
Modified k Nearest Neighbors (kNN)

Despite its simplicity, kNN is probably one of the most effective Machine Learning algorithms. However, one major shortcoming of regular kNN is the use of Euclidean distance, instead of some more advanced metric learning technique. Euclidean distance gives equal weight for each feature, which is very unlikely in large and noisy datasets. In our modified version of kNN, we build N VR-trees using random forest algorithm. After this procedure, we take some specified fraction of features from each tree in the forest and use only those features to calculate Euclidean distance. In other words, the features collected from each tree will correspond to one kNN classifier. If we have built N trees, we will also have N kNN classifiers. Each classifier will vote and the final vote will be determined as an average of the sum of the votes.

Combination (OU) Bet:

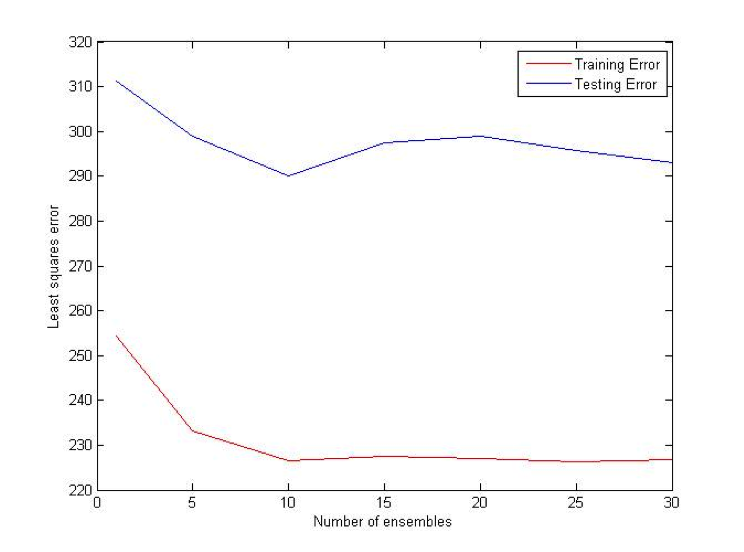
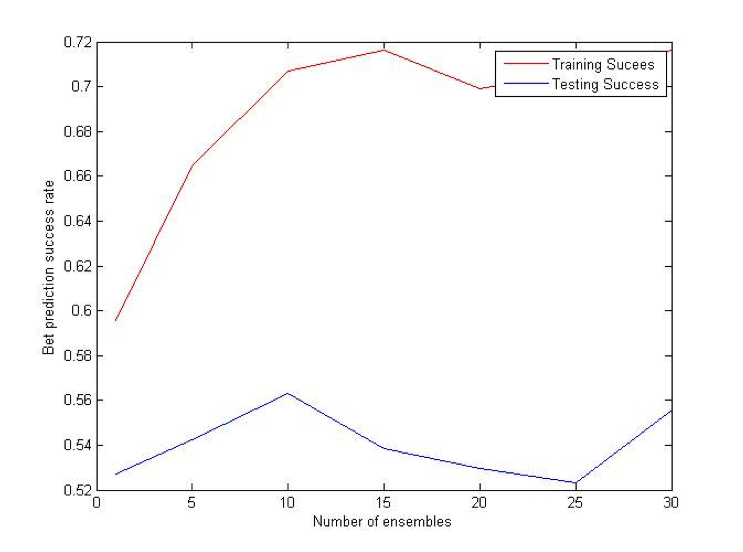
Difference (ATS) Bet:

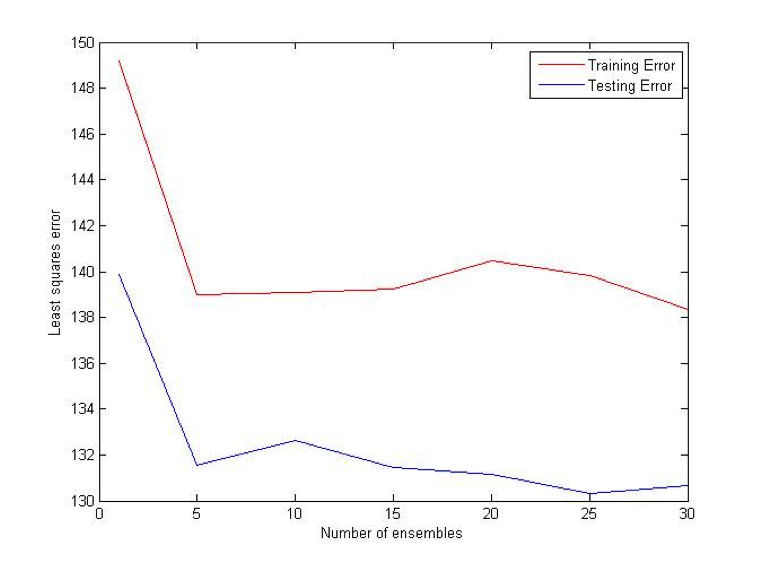
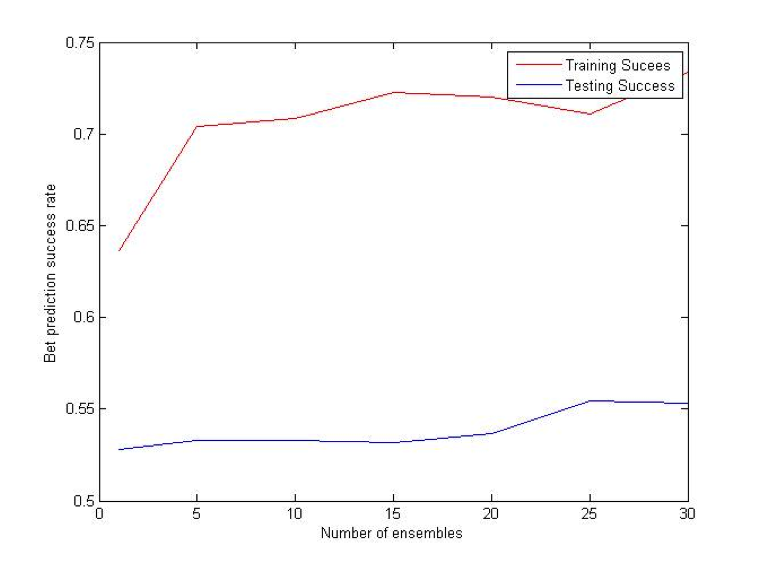
AdaBoostR: AdaBoost for Regression

AdaBoost (adaptive boosting) is a method to generate strong classifiers from a pool of weak classifiers. This is done by iteratively training weak classifiers on a weighted distribution of training examples (currently misclassified examples are weighted higher), and then boosting their weights appropriately so that the weighted sum of their contributions provides an optimal prediction of the target value. [7] While AdaBoost is traditionally used to solve binary classification problems, an extension of AdaBoost called AdaBoost.R can be used to solve regression problems. [8] We implemented the AdaBoostR algorithm described in Zemel & Pitassi (2001).

Weak Learner: Quadratic Least Squares Regression on Subset of Feature Space

The weak learner we are using derived by choosing, on each iteration, a random subset of 10 feature dimensions and performing least squares regression with iterative batch gradient descent on a quadratic basis vector of the input. We will experiment with training on different sized subsets of feature dimensions or on linear basis vectors instead of quadratic ones.

AdaBoostR Algorithm

AdaBoost initially sets all input training examples to uniform weights. Then, until the error term converges to a minimum, a weak learner is trained on the current distribution of training examples. We only accept weak learners that meet our standards after they are trained. Before the weak learner is accepted into the AdaBoost committee, it is tested against a ‘demarcation threshold’ for performance. If it is accepted, the weak learner’s combination coefficient is then set by line search in order to minimize the cost function. The training distribution is then updated based on error, and prediction is represented as the guesses of each weak learner weighted by its own relative combination coefficient.

Challenges and Errors

Currently, our version of AdaBoostR is functional, but does not perform to our standards. AdaBoostR will require more thorough testing before it is completed. Many parameters need to be adjusted, including the regularization term for regression, selecting the type of basis function used, the number of weak learners included and the number of subset features to use in training each weak learner.

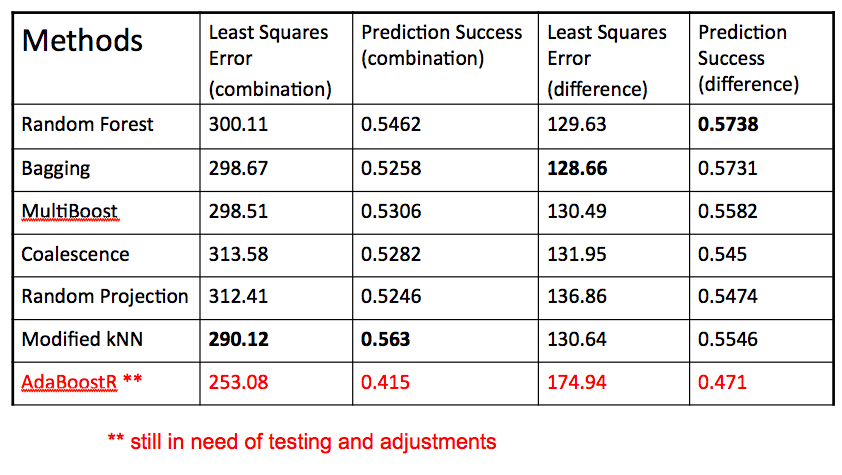
Summary of Results

Remaining Tasks and Future Goals

All algorithms have been implemented and have produced initial results at this point. Our profit threshold goal of 52.63% has been reached and exceeded already. Our current progress is such that the final weeks of the project can be focused solely on fine-tuning and further optimizing the algorithms already implemented. This will involve testing a wide range of threshold values within our implemented methods, which as of now have not been tested for optimal values of constants. For AdaBoostR, we will fix current errors in the existing implementation and we will also be defining a new type of weak learner.

References

[1] Breiman, Leo. Classification and Regression Trees. Belmont, CA: Wadsworth International Group, 1984.
[2] Zhou, Zhi-Hua. Ensemble Methods: Foundations and Algorithms. Boca Raton, FL: Taylor & Francis, 2012.
[3] Liu, Fei Tony, Kai Ming Ting, Yang Yu, and Zhi-Hua Zhou. "Spectrum of Variable-Random Trees." Journal of Artificial Intelligence Research (2008).
[4] Barros, Rodrigo, Ricardo Cerri, Pablo Jaskowiak, and Andre Carvalho. "A Bottom-Up Oblique Decision Tree Induction Algorithm." IEEE (2011).
[5] "Sports Betting Information on Odds Shark." Sports Betting Odds. Web. 21 Jan. 2013.
[6] "ESPN NBA Scoreboard." NBA Basketball Scores. Web. 21 Jan. 2013.
[7] Roja, Raul. “AdaBoost and the Super Bowl of Classifiers: A Tutorial Introduction to Adaptive Boosting.” (2009).
[8] Shrestha, D.L. and Solomatine, D.P. “Experiments with AdaBoost.RT, an Improved Boosting Scheme for Regression.” Neural Computation (2006): 18:7, 1678-1710.
[9] "Reduced Error Pruning." Reduced Error Pruning. N.p., n.d. Web. 21 Jan. 2013.
[10] Webb, Geoffrey. Multiboosting: A Technique for Combining Boosting and Bagging. "Machine Learning" (2000)
[11] Zemel, R. S. and Pitassi, T. A gradient-based boosting algorithm for regression problems. Advances in neural information processing systems (2001), 696-702.