Movie Recommender System
Instructor: Lorenzo Torresani
Yusheng Miao, Yaozhong Kang, Tian Li
{Yusheng.Miao.GR, Yaozhong.Kang.GR, Tian.Li.GR}@Dartmouth.edu
February 19, 2013
Introduction
What movie should you watch tonight? It's really a hard choice since there're so many movies that even scanning their brief introductions will cost us a lot of time. So we do need a personalized recommendation engine to help narrow the universe of potential films to fit our unique tastes. Fortunately, with the help of machine learning technique, it helps users to survive from enormous volume of information and provides valuable advices about what they might be looking for based on their particular information, such as profile, searching history, etc. Product recommendation on Amazon.com is one of those successful examples in this field.
As a matter of fact, there are new movies released even every day, however, comparatively few tools can hlep us organize these content and directly pick those movies that are more likely to interest us. To address this problem, we want to develop a hybrid Movie Recommender System based on Nerual Networks, which takes into consideration the kinds of a movie, the synopsis, the participants (actors, directors, scriptwriters) and the opinoin of other users as well[1], in order to privde more precise recommendations.
Our recommendation process can be shown as the following diagram.
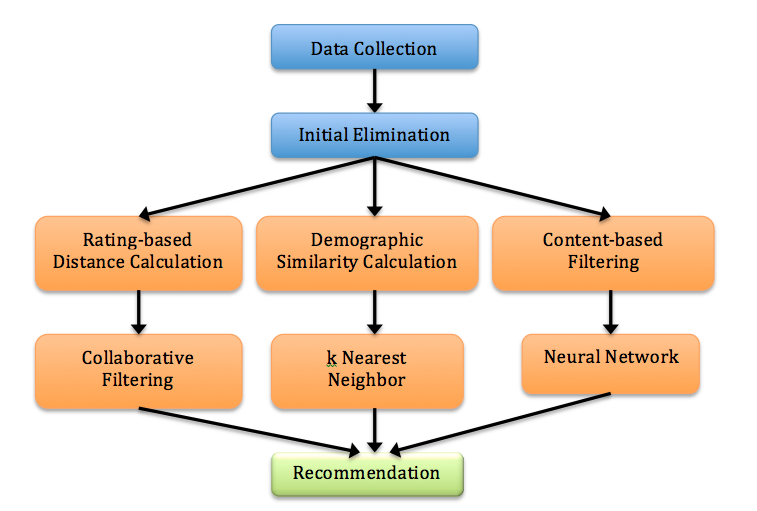
Figure 1
Data Process
In addition to dataset we obtain on
MovieLens, we also crawled the information of directors, writers, actors and plot key words from
IMDB for each movie.
In total, we have:
- 100,000 anonymous ratings (in form of 1-5) from 943 users on 1,682 movies;
- Each user has rated at least 20 movies;
- Simple demographic info for the users, including age, gender, occupation, and zip code;
- 1,068 directors over all these 1,682 movies;
- 1,995 writers over all these 1,682 movies;
- 2,743 actors over all these 1,682 movies;
- 3,403 plot keywords over all these 1,682 movies;
Approaches
Rating-based Filtering
In this rating-based part, we use Pearson Correlation Coefficient to find the correlation between the specific user and the rest of the users[1].
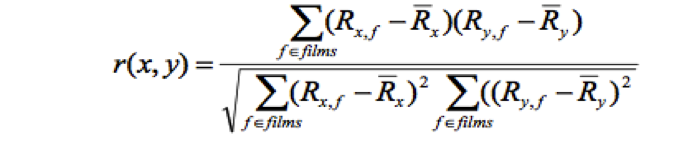
Here R
x,f is the rating of user x for film f, and
stands for the mean value of the rating of user x. Thus, for each user, we find the correlation with all the other users by applying this formula on all the movies watched by both of those two users.
The correlation we got is a decimal number that lies within [-1,1], where -1 stands for the loosest correlation between two users, while 1 stands for the strongest correlation between two users. This accords to the farthest and nearest neighbors of kNN method. In our project, we take into consideration not only the opinion of a user y who has a very strong correlation with user x, but also the opinion from a user y where he or she has a very loose correlation with user x. Because the fact shows that there is a quiet big chance that user x would like the film which disliked by user y with whom they have the opposite opinions.
More specifically, in our project, for each user, we assign a positive counter and a negative counter for each of all the movies. When we have a strong correlation r between user x and user y, and if user y gives a high rating on film f, then the positive counter for this specific user x on this specific movie f will be increased, which indicates that the film f has more chance to be recommend to user x. Obviously, if this user y gives a low rating on film f, then the negative counter for this specific user x on this specific movie f will be increased. As we mentioned above, in our system, we also consider the opinion from a user y who has a loose correlation with user x. Therefore, when we have a loose correlation r between user x and user y, and user y gives a high rating on film f, then the negative counter will be increased indicating that user x might like this movie which disliked by user y. Similarly, the positive counter would be increased on the opposite situation. But, in the loose correlation case, we should note that it does not necessarily mean that user x would like the film disliked by user y, therefore we give a smaller weight on both the positive and negative counters under the loose correlation situation [1].
Finally, we have two counters for each user x on each film f and we recommend films to this user x based on the values of these two counters.
Demographical Filtering
In this part, we utilize the personal information of the users in our dataset. We notice that for each user, there are four attributes, age, gender, occupation and zip code to describe their personal features. We decide to use three of them to further modify our model.
For age and gender, we can define the similarity of two persons on these two attributes as follows[2]:
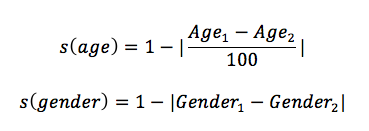
In our dataset, there're 21 kinds of occupations in total. We map them to the model of 6 personality types developed by by John L. Holland in Personality-Job Fit Theory[3]. (The result is shown in Table 1 [4].)
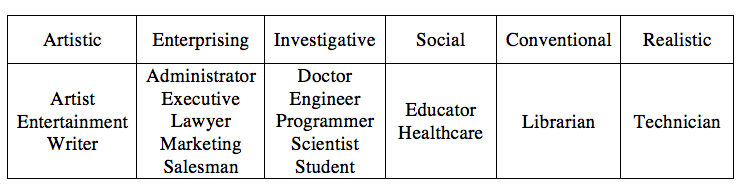
Table 1 The classification of different occupation according to Personality-Job Fit Theory.
Personality-Job Fit Theory also tells us in Figure 2, the similarity of two groups at adjacent positions are larger than those two are separated by one group, and the similarity of the latter one is larger than the two at opposition positions. Thus we calculate the distance between any two groups like this: if two occupations are exact the same, the distance is 0; if the occupations are not same but fall into the same group, we define the distance between them as 1; if the two groups are adjacent, we define distance between them as 2; if they are separated by one other group, we define their distance as 3; if they are at the opposite positions, the distance is defined as 4.
There're also four kinds of occupations (homemaker, retired, other and none) that cannot be mapped to any of these six groups, we just ignore them.
Figure 2 (Source: https://edtechvision.wikispaces.com/file/view/Holland03Jobs.gif)
Our demographical similarity of can be written as follows:
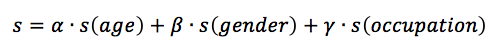
When trying to recommend movies to a certain user, we use the idea of kNN to select those movies with highest average ratings by the k nearest neighbors to the user. This is based on the assumption that people with more similar background tend to share similar interests.
Content-based Filtering
The key idea of content-based filtering in movies recommender system is that some features of the movies influence users' choices. For example, most of us have individual preferences on certain movie types. Some of us like action movies while the others may prefer comedy. The same case appears on movie stars. Users would tend to give a higher rate to those movies acted by their favorite stars.
In additional to movie type that is included in the original dataset, we retrieved some more features about the movies from IMDB by a Web-crawler program, which is written in Java and Python. These features include: (1) Actors (2) Directors (3) Key words. Each of these features is represented by a vector containing 0s and 1s with 1 indicating that a certain Actor/Director/Key word is related to this movie and 0 otherwise.
We extracted 470 actors, 146 directors and 689 key words from the website with each of them appeared in at least 2 movies. Here comes with a problem. For example, if two movies are directed by different directors but both directors are not in the 146 directors we extracted. Then for both of the two movies, the director vectors contain only zero. The system will consider them as the same feature but actually they are not. This problem may damage the overall prediction result. After solving this problem, we expect the error rate to be lower than what the figure shows in the next section.
We constructed four different neural networks for each user corresponding to the four features mentioned above [1]. The training process is based on the sub-matrix, which contains only the movies that the user has evaluated. The size of the training set varies from users since each user has rated different number of movies. To avoid over-fitting, we adjusted the number of neurons in the hidden layer for each user corresponding to the size of the training sample. Here we adopted the Resilient Back Propagation method as the transfer function in our neural network [5].
When a movie comes to a user, each of the four neural networks outputs a value, which is a prediction of how much this user may rate the movie according to the value of the feature. We assume that the weights of these properties are equal. So we take the average score as the predicted score. A more sophisticated way is to use linear regression to determine the weights. However, experiments have shown that linear regression does not bring higher prediction accuracy. The reason might be that there are only dozens of rating records for many of the users and thus a sophisticated model may cause over-fitting on the training set. Finally, we sorted the score and picked out fixed number of movies with the highest scores to recommend to the user.
Experiment
In our experiment, we first test the error rates of using the three methods mentioned above respectively. Here we define two criterions to evaluate the error rates. The first one is Like-but-Not-Recommend (l-nr in Figure 3) meaning that the movies user likes but are not on our recommendation list; the second one is Dislike-but-Recommend (d-r in Figure 3) which means that we recommend the movies that user doesn't like.
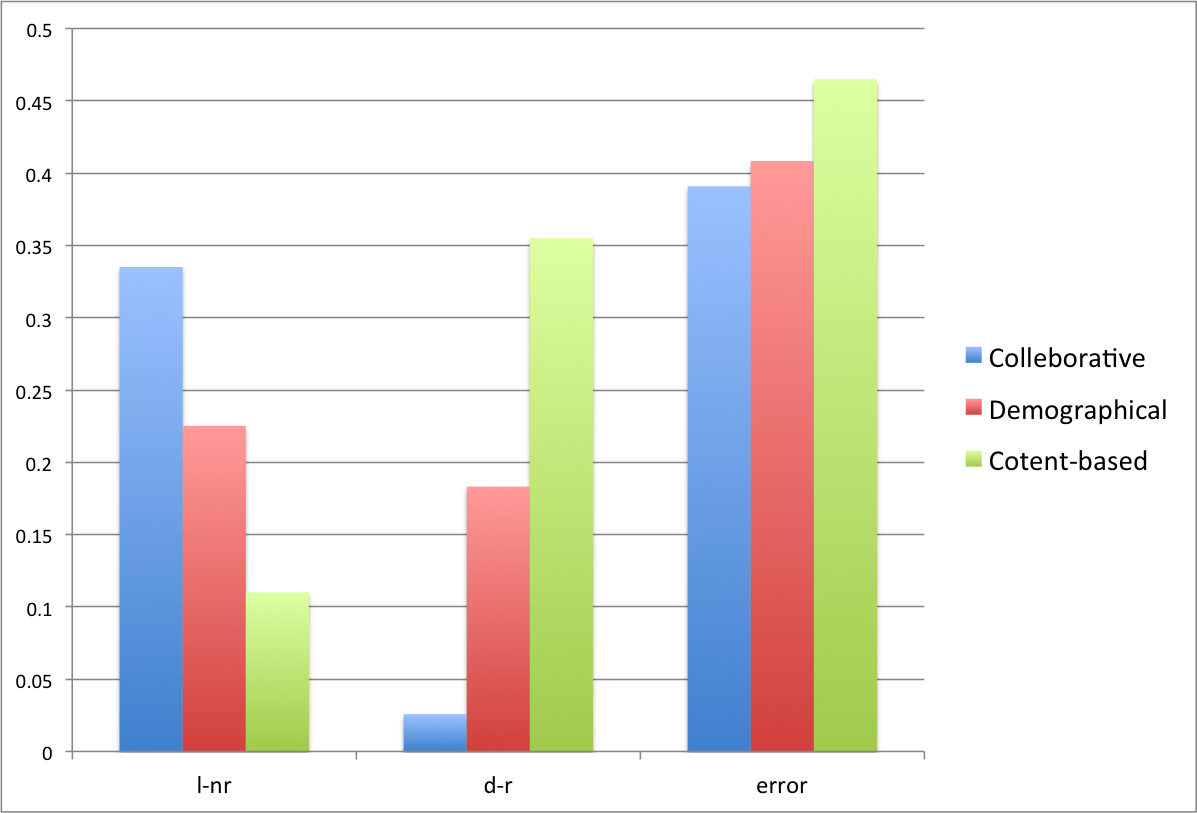
Figure 3: The error rates of using the three methods respectively.
We also combine the three methods together to generate a recommendation list for each user. We test the precision rate on different number of recommendations, our precision rate defined as following:

We first let each method recommend 3 movies for each user, and test the precision rate, which is roughly 75%, and then we increase the number of movies recommended by our method, where we use 5, 10, 15 and 20. The results are shown as below:
From this figure, we can know that along with the increases in the number of movies recommended, the precision rate decreased. For example, when we recommend 5 movies to each user and the precision rate is roughly 70%, but when we recommend 10 movies to each user, the precision rate is only 55%. However, we should note that, in practice, we cannot recommend all the films that the user would probably like, because this would lead us to the problem of infinite choices, therefore, it makes sense that we let our hybrid system recommends 5 movies to each user where we can guarantee that the precision rate is 70%.
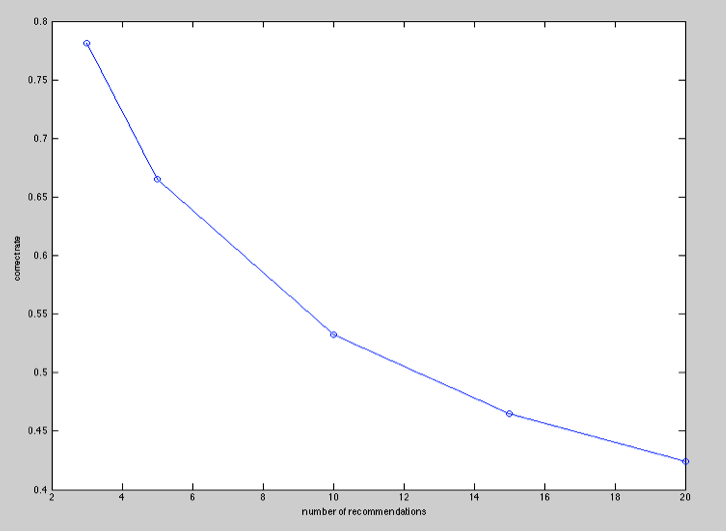
Figure 4: x-axis represents the number of recommendations, y-axis represents the precision rate.
References
[1]. Christina Christakou, Andreas Stafylopatis, "A Hybrid Movie Recommender System Based on Nerual Networks", isda, pp.500-505, 5th International Conference on Intelligent Systems Design and Applications (ISDA'05), 2005
[2]. Umanka Hebbar Karkada, Friend Recommender System for Social Networks.
[3]. Personality-Job Fit Theory.
http://en.wikipedia.org/wiki/Personality%E2%80%93job_fit_theory
[4]. Holland Codes.
http://en.wikipedia.org/wiki/Holland_Codes
[5]. Anil K. Jain, Jianchang Mao, K. M. Mohiuddin. Artificial Neural Network: A Toturial. Computer, Volume 29, Issue 3, pp.31-44. Mar, 1996.

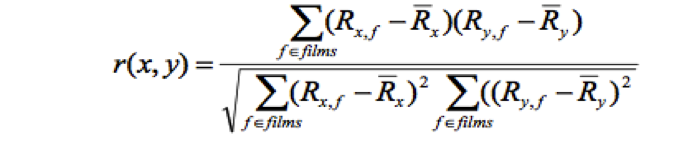 Here Rx,f is the rating of user x for film f, and
Here Rx,f is the rating of user x for film f, and  stands for the mean value of the rating of user x. Thus, for each user, we find the correlation with all the other users by applying this formula on all the movies watched by both of those two users.
stands for the mean value of the rating of user x. Thus, for each user, we find the correlation with all the other users by applying this formula on all the movies watched by both of those two users.
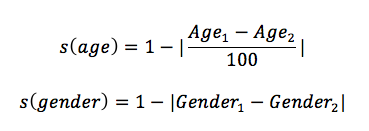


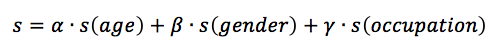 When trying to recommend movies to a certain user, we use the idea of kNN to select those movies with highest average ratings by the k nearest neighbors to the user. This is based on the assumption that people with more similar background tend to share similar interests.
When trying to recommend movies to a certain user, we use the idea of kNN to select those movies with highest average ratings by the k nearest neighbors to the user. This is based on the assumption that people with more similar background tend to share similar interests.

 We first let each method recommend 3 movies for each user, and test the precision rate, which is roughly 75%, and then we increase the number of movies recommended by our method, where we use 5, 10, 15 and 20. The results are shown as below:
We first let each method recommend 3 movies for each user, and test the precision rate, which is roughly 75%, and then we increase the number of movies recommended by our method, where we use 5, 10, 15 and 20. The results are shown as below:
