
We aim to build a model that will predict whether a novel will be successful or not. Previous research has generated accuracies of up to 84% using SVM's [1]. We approach the same problem using random forests on a selection of linguistic features such as vocabulary and syntax.
We have accomplished our milestone goal of implementing the random forests algorithm using a number of baseline features. Our process and results are detailed below.
In order to directly compare results with [1], we use the same dataset from the Project Gutenberg database of novels available at [2]. The dataset is organized by genre (Adventure Stories, Fiction, Historical Fiction, Love Stories, Mystery, Science Fiction, and Short Stories), with each genre containing 100 novels (half success, half failure) for a total of 700 novels overall.
We use the download count of a novel from Project Gutenberg as the metric for success. Following [1], novels with over 80 downloads are classified as successes while novels with under 25 downloads are classified as failures. Success novels have a median of 225 downloads while failure novels have a median of 10 downloads. Training and test set comprise 80% and 20% of the data respectively and we perform four-fold cross-validation on the training set.
We use unigrams with tf-idf, deciding not to use bigrams or tf-idf bigrams as they turned out to be both computationally expensive and uninformative. We further narrow down the feature space of unigrams by using tree-based feature selection to select the top 100 most informative unigrams.
In addition we use a variety of features ranging from simple metrics such as the average number of words per sentence and the average word length to more linguistically informed features such as average number of POS (part-of-speech) tags per sentence. POS tags are generated according to the tags outlined in the Penn Treebank Project [3].
As mentioned in our proposal, the learning algorithm of choice for us was the random forest learning algorithm. We separate the construction of random forests into two steps: building individual decision trees and inserting randomness in how all trees are grown in order to obtain a well-varied forest of trees.
The algorithm we wrote for building individual decision trees was the bulk of our implementation. The core part of growing these trees is deciding which feature to "branch" on during learning, and there are a number of metrics to do this. Among the most common are the Gini impurity metric and information gain metric. We choose the latter metric, which makes our algorithm very similar to the ID3 or C5.0 decision tree algorithms.
Our algorithm works by first determining the best feature to branch on using the information gain metric in Figure 1 below. Since all of our features at this point are continuous, for each individual feature we must also iterate over all unique values of that feature to determine which value to "split" on, i.e. if we were to branch on a feature, we would determine the best y such that for feature x, x <= y and x > y split the data into two groups so that entropy is minimized. After finding the best split for each feature, we obtain the best feature to branch on and can recursively repeat this process until our tree reaches a certain depth or until entropy can no longer be further minimized.

We insert randomness into the construction of each decision tree in two ways. The first method is through bagging: before constructing each tree, we randomly select a fraction of the data (with or without replacement) for the tree to be trained on. The second method is by randomly constraining the features that can be selected at each branch of the decision tree.
We currently have four-fold results on our training data. In addition to our own random forest implementation, we provide the default implementations for random forests and SVM's, found in the Python sklearn library, as benchmark comparisons. We have not yet tuned on any of the learning algorithms.
Charts 2 and 3 show our preliminary results. We can see that our self-built random forest implementation performs very similarly to the built-in random forest, and both models consistently outperform the SVM implementation. Notably, the random forest implementation has a similar accuracy when predicting either successes or failures, while the SVM model consistently biases towards predicting successes and thus has less than 50% accuracy overall in classifying failures.
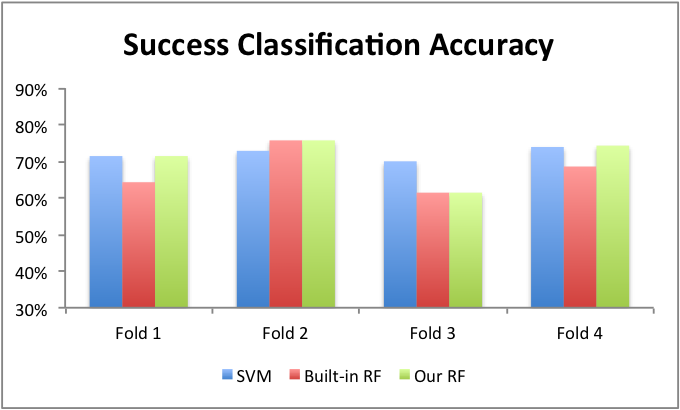
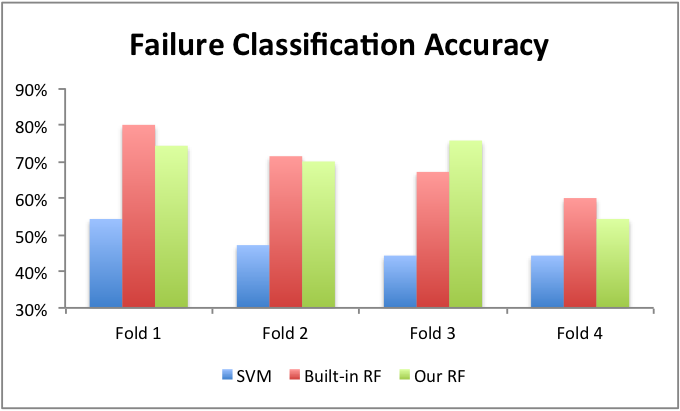
Table 4 shows some of the unigrams that were determined to be most important in our random forest model based information gain. As only a few unigrams (though, new, brought, began, end, having) ever reappeared in the top 100 most important unigrams, we believe that unigrams are only important as a whole and it is difficult to narrow down a small subset of unigrams that are especially important in predicting literary success.

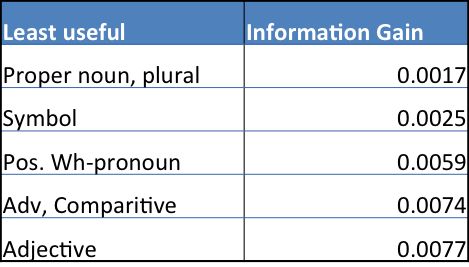
In attempt to give some color to other features that are important, we show in Table 5 the most important non-unigram features ranked by information gain in our models and in Table 6 the non-unigram features which provide the least information gain.

Currently we are testing on a standard selection of features based on vocabulary and word-level syntax. We plan on expanding our feature set by adding more potentially meaningful features such as sentence-level syntax, following [5]. For example, the average number of subordinate clauses per sentence may indicate more sophisticated sentence structure which could positively correlate with a novel's success. We also plan on using Latent Dirichlet Analysis (LDA), which will provide a measure of how content rather than writing style affects success, along with the genre of each piece of fiction. Finally, readability metrics may also be useful, as they could be correlated with how enjoyable a novel is to read.
Although random forests do not typically require as much tuning as other learning models, we still have a few parameters to tune: the maximum depth we allow an individual decision tree to grow until, the fraction of data we use in bagging the trees, whether or not we do bagging with replacement, and finally, the number of features we randomly designate as candidates when determining the best feature to "branch" on for a decision tree. We already have four folds of data within our training set that will be used for this cross-validation.
[1] Vikas Ganjigunte Ashok, Song Feng, and Yejin Choi. 2013. Success with style: Using writing style to predict the success of novels. In Proceedings of EMNLP. [2] Success With Style Project [3] Penn Treebank POS Tags [4] http://www.cs.cmu.edu/afs/cs/project/theo-20/www/mlbook/ch3.pdf [5] Emily Pitler and Ani Nenkova. 2008. Revisiting readability: A unified framework for predicting text quality. In Proceedings of the 2008 Conference on Empirical Methods in Natural Language Processing.