About Schedule Software

PS-2, due Apr 21

Introduction

Suppose we have a bunch of animated blobs. How can we determine if the mouse was pressed in one of them? How can we detect when two of them bump into each other? We've seen the inefficient approach to determining which was clicked on — test each one. And we can imagine an inefficient approach to detecting collisions — look at all pairs. But we can do better, and would need to do better in some applications requiring speed.

Just as a binary search tree enables faster look-up than linear search in one dimension (based on some notion of less than or greater than), a point quadtree enables faster look-up in two dimensions. The structure is like a BST: each node stores an element, and then has children recursively storing additional elements based on how they compare to the parent. But now there are up to four children, in the four quadrants:

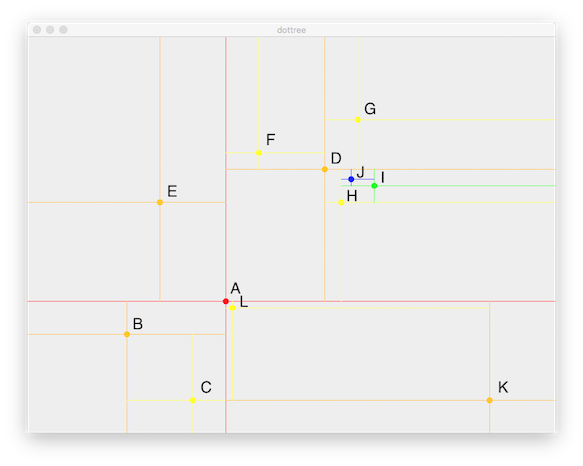
Here A is the root, and it has children B (lower left), E (upper left), and D (upper right), and K (lower right). B has only one child C (lower right), while D has three children F (upper left), G (upper right), and H (lower right). H has one child I (upper right), which itself has one child J (upper left). Finally, K has one child L (upper left).

Note: there are several variations on the idea of a quadtree; we're following here an extension of the classic approach described by Finkel and Bentley in "Quad Trees: A Data Structure for Retrieval on Composite Keys", Acta Informatica 4, 1—9, 1974. See Fig. 1 for another example, also drawn as a tree. The paper is a good read, though I've translated some of the ALGOL-like description to pseudocode here, and used recursion rather than iteration. Be careful searching the web for further descriptions, as you might end up implementing an extra credit quadtree instead of the assigned one!

Data Structure

We want our quadtree to be generic to what "points" it holds, as long as they provide the ability to get x and y coordinates. Thus we have a new interface Point2D specifying those methods. We then modify Blob to indicate that it implements that interface, and to emphasize the generic-ness we also use a simple class Dot that basically just meets the interface specification.

The basic data structure that we'll use for each node in the tree includes:

• a point, of generic type E, as long as it implements the Point2D interface (so we can get coordinates)
• the two corners, upper-left (x1,y1) and lower-right (x2,y2), of the rectangle that the node covers. (It isn't really necessary to store these, but it makes our life easier.)
• Four PointQuadtree children, one for each quadrant, numbered as in the figure. Any quadrant may be empty, in which case the child is null.

So the main tree covers (x1,y1) to (x2,y2), while its upper-right quadrant #1 covers (x,y1) to (x2,y), and so forth. Make sure you agree with this. Note: I'm sticking with the graphics convention of the origin at the upper-left, and smaller y values higher up in the image. This makes computing these things with < and > feel a little strange compared to our math intuition, but oh well, such is graphics.

Insertion

Inserting a point works much like for a BST (except with four children instead of two): at a given node, see which side (quadrant) the point lies on, and recursively insert in the appropriate child. When there is no child for that quadrant, create a new leaf containing just the point, and store that leaf as that child.

To insert point p, which is at (x,y)
  If (x,y) is in quadrant 1
    If child 1 exists, then insert p in child 1
    Else set child 1 to a new tree holding just p
  And similarly with the other quadrants / children

Finding

Finding in the tree is similar to finding in BST, with one important difference (in addition to number of children): typically here we want to find all points within some region of interest, not just a single value. For example, the mouse might not be pressed exactly where a point is, but if it's close enough, we'll consider it a hit. Thus we search in a circle around the mouse location. Similarly, to detect collisions, we search in a circle around a given blob to see if another blob is too close. So the recursive call for find considers all children whose rectangles overlap the region of interest.

So let's consider how to find all objects within a circle. We'll assume that we have methods to see if a point is inside a circle, and to see if a circle intersects a rectangle.

To find all points within the circle (cx,cy,cr), stored in a tree covering rectangle (x1,y1)-(x2,y2)
  If the circle intersects the rectangle
    If the tree's point is in the circle, then the blob is a "hit" 
    For each quadrant with a child
      Recurse with that child

Here are some example search circles in the above picture; make sure you're comfortable with what rectangles get checked and what tree points get checked:

• Searching in a circle near where B is. Start at the root, A, and see that the circle intersects its rectangle. In this case the circle around the point we are searching does intersect the rectangle, because A's rectangle is the entire board. Test the point to see if A is inside the circle around the point we are searching — not a hit, the search point is too far away. Recurse to A's children D, E, B, and K. The circle only intersects B's rectangle. Check B's point; it is a hit, the search point is close to B. Also recurse with B's child C to see if more than point is in the search circle. The circle intersects C's rectangle. Check C's point; not a hit.
• Searching in a circle near where G is. Start at the root, A, and see that the circle intersects A's rectangle. Test its point, not a hit. Recurse to A's children D, E, B, and K. The circle only intersects D's rectangle. Check D's point; not a hit. Also recurse with its children G, F, and H. The circle only intersects G's rectangle. Check G's point; it is a hit.
• Searching in a circle near where A is (big enough to also contain L). Start at A, circle intersects A's rectangle, point is a hit. Recurse to children D, E, B, and K. Circle intersects all of their rectangles but doesn't contain any of their points. Further recursion from these tests G, F, H, C, and L. Only L's rectangle intersects. And its point is also a hit.

(Note: these are the first three test cases in test1 of the provided DotTreeGUI.)

Applications

This data structure and search mechanism then lets us solve the problem of quickly finding blobs near the mouse press — search in a circle around it.

When we move from points to blobs of some size for collision detection, we actually have to account for that size. Blobs intersect when their sides touch each other, not their centers. While in general, a point quadtree is only supposed to contain points (with variations developed to allow regions that have some extent in space), we can handle it here with a little trick. Let's deal only with blobs of a common, fixed radius. Then we can simply expand the circle we're looking for by that same amount and look for a point (e.g., blob 1 has radius r, blob 2 and all other blobs also have radius r, so by looking for other blobs within 2r of blob1 we will detect any other nearby blob).

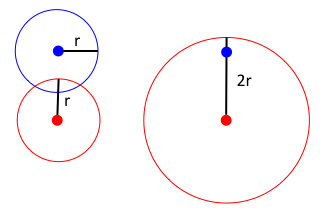
Now we can efficiently solve collision detection. Insert all the blobs into a tree. For each blob, find all other blobs within a circle of radius twice that of one blob.

Implementation Notes

A bunch of files are provided for you: ps2.zip. There is a scaffold for the PointQuadree class. The Point2D interface is implemented by the simple Dot implementation, and by a slight modification to Blob indicating that it implements the interface. A Geometry class provides two static methods for the geometry tests, instrumented to keep track of how many times each is called. The DotTreeGUI helps you test your point quadtree implementation graphically (insert points and see what's near the mouse) and with some hard-coded test cases. Finally the CollisionGUI sets up a bunch of colliding blobs.

PointQuadtree

• The code is quite analogous to BST, so familiarize yourself well with that first. It is recursive, with data structure recursion — from a node to its children.
• In order to build up a list over the course of recursion, a helper function is useful. Refer back to the fringe of a binary tree.

Geometry

• Helper functions are provided for testing point-in-circle and circle-intersects-rectangle.
• Note that the functions increment static variables, which hold their values over all calls, and thus allow us to count the number of calls. Methods allow other classes to reset and access the counts. This is used in the DotTreeGUI to compare the number of calls your code makes to the idea number.

DotTreeGUI

• The GUI has two modes: 'a' for add to the tree and 'q' for query the tree to find blobs near the mouse press. It also allows you to grow/shrink the size of the circle around the mouse, in which you're detecting blobs.
• There are some test cases that create pre-specified trees and perform searches on them, seeing how many nodes your tree search returns, and how many geometry tests it does along the way.
• The drawTree method is outside the PointQuadtree class, so we explicitly pass around a tree object (and recurse with its children).

CollisionGUI

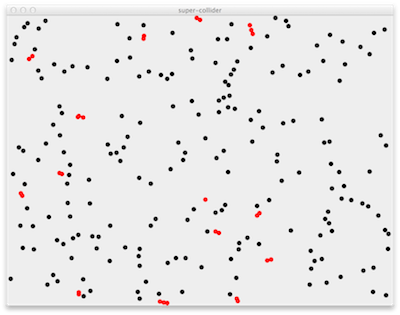
• The core of the GUI is much like BlobsGUI, except that only a couple of blob types (with fixed radius) are included. Also a bunch of blobs at random positions can be added at once (key 'r').
• There are two collision-handling modes: either just color the colliding blobs differently (key 'c', picture below from sample solution) or actually destroy them upon collision (key 'd'). The functionality is based on the findColliders method, which sets the colliders instance variable. Destruction takes advantage of the removeAll method of lists.
• To build a tree with all the blobs, create a new instance holding just blob number 0, and then add blobs 1.. to it.
• As described above, to check collisions, do a find around a blob. Note that this will find the blob itself, since it's in the tree. That's okay, just handle it carefully.

Exercises

For this problem set, you are allowed to work with one partner. Note that you do not have to work with a partner, and if you do, you will both be given the same grade; there is no penalty (or bonus). You should weigh whether you will get more out of this assignment working alone or with someone else. If you choose to work with someone else, pick your partner carefully, and make sure it is someone you will be able to coordinate with, work well with, etc. Re-read the course policies.

1. Implement the PointQuadtree methods. Insert is of course first, but size and even allPoints should come along soon after, to help test. Note that you can (and should) do some testing of these even before tackling findInCircle.
2. Implement the DotTreeGUI methods, to enable graphical construction and viewing of your trees.
3. Exercise your tree code by inserting points in different patterns (including the one illustrated above), checking that it displays correctly and that the mouse press picks up the points that it should (and doesn't pick up others). Note that you can expand/contract the mouse radius with +/- keys. Write a test2 method that codifies some of your test cases. That is, it creates a tree and does some searches on the tree, comparing expected to actual results. You can use my testFind method if you like, or just do something simpler, e.g., comparing the points found to what you think should be found. In your write-up describe these test cases.
4. Implement the CollisionGUI methods.
5. Test your collision detection method by eye in an ad hoc fashion, as well as by devising careful test cases of things that should collide and things that should not. Take a screenshot of color-coded collisions (as above) and briefly describe your tests.

You may obtain extra credit for extending and enhancing the app. Only do this once you are completely finished with the specified version. Make a different file for the extra credit version, and document what you did and how it works. Some ideas:

• Extend the DotTreeGUI to show the nodes tested in trying to find the mouse press location.
• Implement a find-in-rectangle method.
• Let the user drag out a circle (or rectangle) and show the points in it.
• Extend CollisionGUI to handle additional blob types.
• Allow for blobs with variable radii, correctly accounting for how they must be searched.
• Implement a point-region quadtree, which uses a uniform spatial subdivision and keeps points within these quadrants.

Submission Instructions

Turn in your completed versions of the three classes. Turn in screenshots of your GUIs and a document with your dicussion of tests.

Grading Rubric

Total of 100 points

Correctness (70 points)

10	PointQuadtree insert
5	PointQuadtree size
5	PointQuadtree allPoints
10	PointQuadtree findInCircle
5	DotTeeGUI mouse press invoking PointQuadtree to add, find
10	DotTreeGUI draw tree
5	CollisionGUI find colliders: build the tree
10	CollisionGUI find colliders: find all of them
10	CollisionGUI draw to show colliders

Structure (10 points)

4	Good decomposition of and within methods
3	Proper used of instance and local variables
3	Proper use of parameters

Style (10 points)

3	Comments for new methods (purpose, parameters, what is returned)
4	Good names for methods, variables, parameters
3	Layout (blank lines, indentation, no line wraps, etc.)

Testing (10 points)

5	Testing PointQuadtreeGUI
5	Testing CollisionGUI