State space
We saw that search techniques can apply to implicit graphs as well as explicit ones, e.g., when we discover the vertices and edges of a maze as we go along. More generally, we can search any "space" where we can move from one "state" to another. For example, in robotics, we can search from one configuration of arm joints to another, in order to pick up something. Today we'll look at searching other state spaces.
Backtracking
Sometimes instead of finding a single path or a single solution we want to find all solutions. A systematic way of doing this is called backtracking. It is a variant on DFS on an implicit graph. Typical approach: recursion. At every choice point, have a loop to go through all choices. For each choice, call yourself recursively. Succeed if you find a solution, fail otherwise and backtrack to try an alternative.
search(partialSolution) {
if partialSolution is a complete solution
print partialSolution or add it to a list of solutions
else
for all ways to extend partialSolution by one step
modify partialSolution by applying the step
if extended partialSolution is valid
search(partialSolution)
if necessary, undo the step
}See the same recursive DFS structure here? (Could you write a stack-based version?) It's just that there's not an explicit graph telling us which edges to consider — instead we look at possible extensions on the fly and decide which are valid. We'll use this basic search approach to explore implicit search spaces (i.e., where the graph is never really constructed).
Sudoku
Challenge for you: "Prime Minister of Singapore shares his C++ code for Sudoku solver". He implemented a backtracking based search. We won't go over his C++ code (though I bet you can read it), or the many Java codes out there, but the problem presents a nice example of backtracking.
Most of you probably know Sudoku: 9x9 puzzle; some numbers filled in; fill in remaining with numbers 1..9; cannot repeat number in row, column, or 3x3 "box".
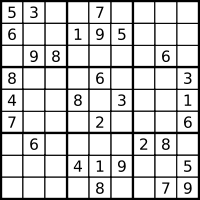
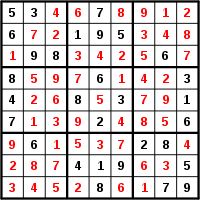
Sudoku puzzle (left) and with solution in red (right) [images are from Wikimedia commons and are in the public domain]
Naive solution: try each combination of numbers, see which satisfies the requirement. If n empty cells, then 9n different combos — slow! But you'd never try it this way yourself, so let's attempt to be a little smarter here, too.
Think of it as a graph, where each node is a board (maybe just partially filled in). From one board we can go to another board by filling in one number, so that "filling in" process is like an edge between the board vertices. So now we need to find a path from the start board to some valid (by the rules of the game) destination board. We don't want to enumerate all the boards up front, to make an explicit graph, so the graph is implicit, with nodes being constructed on the fly as we explore outward from the initial board by filling in a cell at a time.
The question then is in which "direction" do we expand from a given board, i.e., which cell do we try filling in, with which value. The not-quite-as-naive solution expands from one board by picking an empty cell and considering all 9 neighbors, with each of the 9 possible values filled into that cell. One of them will lead us to a solution, so we're basically just doing blind search.
But of course not all paths are really worth going down. When considering putting a certain number in a certain cell, we should make sure that it's valid — not already used in that cell's row, column, or 3x3 box. This process is called pruning, and is at the heart of backtracking search. The graph is implicit, so we generate possible states (vertices) on the fly, based on steps (edges) from the current state (vertex), and get rid of those not worth further consideration.
Why is this called pruning? Because we can view the search as a tree (the path from the root to any node in the tree represents a partial solution, making a particular choice at each step). Rejecting an invalid partial solution corresponds to lopping off its node and the entire subtree that would go below it. So we have "pruned" the search tree. Thus early pruning lops off large subtrees. Effort spent pruning usually (but not always) pays off in the end, because of the exponential growth in number of solutions considered each time a choice is made.
Pruning invalid solutions is sufficient to enable solving of many Sudoku puzzles, just via a blind search like approach, keeping a collection of states to visit, and visiting each by expanding to its neighbors and putting the valid ones into the collection.
Additional knowledge can be brought to bear to identify which cell to expand in a given board state. For example, when there's only one empty cell in a given row, it's completely constrained and we might as well fill it in. If we don't just fill in the states in order, but apply such insights, we can be much more efficient in our exploration. (We do then have to be careful about redunandancy, as we could arrive at the same state via different paths, but we already know how to deal with that from blind search.) And there are other ways to define the states that feel a bit more like a human solver; e.g., a state holds all the possible values for each cell (some of which have been fixed to exactly one value). But the basic algorithm is the same.
Subset Sum
Suppose we are given a list of positive integers (with no repetitions) and a target number. The goal is to find all subsets of the integers that sum to the target.
So what is a "step"? It is to decide whether to add the next number in the list to the subset or not. So we will make two recursive calls, one where add the next number to the subset and one where we do not. A complete solution is one that sums to the target. A solution is still valid if the sum is at most the target. (Because the integers are all positive there is no way to extend a subset to get a solution if the sum is already too large.)
Code: SubsetSum.java
N-Queens
Idea: place n queens on an n x n chessboard so that no two queens can capture one another. (Two queens can capture one another if they are in the same row, column, or diagonal.) Go column by column. First place a queen in the first row of the first column. Then place a queen in the first row, second column. Continue. Example for 8 queens (image from Wikimedia Commons):
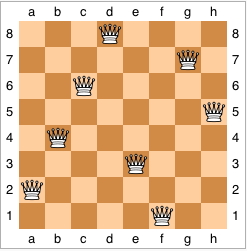
Problem: very slow. Get nn possible solutions (n choices, each with n possible placements). However, we are being really stupid to try to solve the problem this way. As soon as we place the second queen in the first row we can see that it conflicts with the first queen. There is no reason to examine the nn-2 possible solutions that start this way. We forget them and go on to place the second queen in the second row, but that won't work either. So we place it in the third row. Now things are OK (at least so far), and we can move onto the third column. But all 4 positions in the third column are in conflict with one queen or the other, so we place the second queen in the fourth row, etc.
This is the use of pruning here. At kth step we still try to extend the partial solution with (k-1) queens by adding a queen in the kth column in all possible positions. But "possible" now means positions that don't conflict with earlier queen placements. It may be that no choices are possible. In that case the partial solution is not extended, and we backtrack.