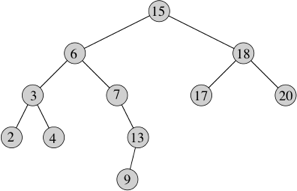
When we visit the nodes in a rooted tree, we are traversing the tree. Of the many possible orders for visiting nodes, three are most common. We think of them recursively, in terms of when to visit a node and when to visit its subtrees. We'll show examples in terms of this binary search tree, where we imagine visiting a node as printing out its key:

These are basic approaches to designing tree algorithms. You are not limited to them. The book talks about an Eulerian tour of a binary tree. It even implements a template that visits each node three times (before its children, between its children, and after its children). The code supplies three methods for you to fill in called left, below, and right. I would have called them before, between, and after. But the idea is that you can be very flexible in how you traverse a tree. (I sometimes find it easier to write the whole traversal rather than fill in the template methods, but it is a matter of taste.) Eulerian traversals definitely abstract the idea of a traversal!
Going back to our binary tree code in BinaryTree.java, we see methods preorder, inorder, and postorder. Each appends data from a subtree to a List. But List is an interface, and in the driver, you can see that it's actually implemented by a Java LinkedList. Here's the preorder method:
public void preorder(List<E> dataList) {
dataList.add(data);
if (this.hasLeft())
left.preorder(dataList); // recurse on left child
if (this.hasRight())
right.preorder(dataList); // recurse on right child
}The other two methods just move the call to add to different locations in the code:
public void inorder(List<E> dataList) {
if (this.hasLeft())
left.inorder(dataList); // recurse on left child
dataList.add(data);
if (this.hasRight())
right.inorder(dataList); // recurse on right child
}
public void postorder(List<E> dataList) {
if (this.hasLeft())
left.postorder(dataList); // recurse on left child
if (this.hasRight())
right.postorder(dataList); // recurse on right child
dataList.add(data);
}Traversing rooted trees comes up quite often. For example, the TreeSet implementation of the Set interface stores information in a binary search tree, and the iterator returned by its iterator method is guaranteed to iterate over the set elements in increasing order. Not surprisingly, this iterator traverses the binary search tree using an inorder traversal.
There's another interesting use of traversals in binary trees. If all keys are distinct and you have both a preorder and an inorder traversal, you can reconstruct the entire binary tree. The method reconstructTree in the BinaryTree class does so. How does this method work? The first node in a preorder traversal is the root. The root is somewhere in the middle of an inorder traversal, with everything in its left subtree before it and everything in its right subtree after it. In the preorder traversal, all of the nodes in the left subtree are visited before anything in the right subtree. So we can build the tree recursively as follows:
leftPre in the code) and one list from the inorder traversal (leftIn in the code). Do so by iterating through the preorder and inorder lists until getting to the root in the inorder list.leftPre and leftIn lists, use them to recursively build the left subtree.rightPre in the code) and one list from the inorder traversal (rightIn in the code). Do so by iterating through the remainder of the preorder and inorder lists, starting from where we left off in step 1 and jumping over the root in the inorder list.rightPre and rightIn lists, use them to recursively build the right subtree.How long does it take to traverse a rooted tree with n nodes? The answer is Θ(n) time. Here's an easy way to see it. We have to consider each edge twice. The first time is when we traverse the edge from the parent down to a child. The second time is when we traverse the edge from the child back to the parent. Conceptually, there is also an edge down into the root, representing the work performed in the initial call of the method. How many edges are there? It is a fact that in any tree—whether or not we think of it as a rooted tree—the number of edges is n − 1. Add in one more for the edge down to the root, and conceptually, there are n edges, each traversed twice. That makes the total time Θ(n).
We can think of expressions as being represented by trees. To keep things simple so that we don't have to think about operator precedence, let's consider only fully parenthesized expressions. Take the expression ((17.5 + (5.0 / x)) * (y - 4.0)). We can represent it by this binary tree:
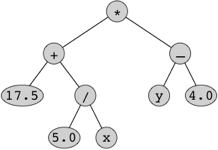
Although we could build an expression tree on top of the binary tree code, we will write a new set of classes to represent expression trees. Each node will be its own type, so that we'll have nodes for variables, constants, and each of the binary operators. We won't include unary operators (such as unary minus) or ternary operators (such as the ? : operator of Java), but we could—and we could not include unary operators if all expression trees had to be binary trees.
The code for expression trees is in this zip file. (I will show you individual classes, but this is the easy way to download the whole thing.) First, look at Expression.java. It is an interface that says that an Expression must provide two methods: eval and deriv. The eval method evaluates an expression and returns its value in a double. The deriv method returns an expression that is the symbolic version of the derivative with respect to a particular variable. An Expression should also override toString.
Next, look at Constant.java. To use a constant, you call its define method, just giving a double with the value of the constant. The define method is static and calls the constructor, which is private, so that the only way to define a constant is by calling define. The constructor just saves the value of the constant in the instance variable myValue, and then the define method returns a reference to the Constant object. Because Constant implements Expression, anywhere you have declared a reference to an Expression, the reference may actually be to a Constant. The eval method just returns the value in myValue, and the deriv method always returns a constant whose value is 0.0, since the derivative of a constant with respect to any variable is 0. The toString method just returns the String representation of myValue.
This scheme, where the constructor is private and there is a static method that calls the constructor is a variant of a design pattern called the factory pattern. Instead of constructing objects directly, users of the class have to go through a method to create an object. One use is to allow the factory to decide to create a subclass object when asked to create a superclass object. Another is to give the user options on what parameters to pass to create the object. For example, complex numbers can be represented using polar or rectangular coordinates. Either way you present two double values, and so you cannot overload the constructor to accept either representation. You can create two factories, however, one of which expects polar coordinates and the other of which expects rectangular coordinates. For example:
class Complex {
public static Complex fromCartesian(double real, double imag) {
return new Complex(real, imag);
}
public static Complex fromPolar(double mag, double phase) {
return new Complex(mag * cos(phase), mag * sin(phase));
}
private Complex(double a, double b) {
// Code to store into private instance variables goes here.
}
}
Complex c = Complex.fromPolar(1, pi);It is less clear why we would want to use this pattern in the Constant class, but it will become clearer later.
The Variable class in Variable.java class is similar, but it has a symbol table to save variable values. These are saved in a Map that is implemented using a HashMap.
We will look at maps in detail later, but for now all that you need to know is that put(key, value) adds the (key, value) pair into the map, get(key) returns the value corresponding to key, and containsKey(key) returns true if the key is in the map.
Note that the
symbolTable is static, so it is a class variable. We have
only one symbol table shared by all of the variables.
As we saw in Constant the constructor is private and there's a define method, but this time it is overloaded. The two-parameter form takes the name of a variable as a String and a value for the variable, storing the name and value in the symbol table. The one-parameter form takes just the name of the variable, and it stores the name in the symbol table with null for the value. A variable whose value is null is defined but uninitialized. The constructor, called by both define methods, stores the variable's name in the instance variable myName. There is an assign method that stores the value in the symbol table entry for the variable. The eval method looks up the variable in the symbol table, using myName as the key, and it returns the value found in the symbol table for the key given by myName. The deriv method determines whether the variable v given as the parameter matches myName. If it does, then the derivative is 1; otherwise, the derivative is 0. The correct Constant is defined and returned in either case. The toString method just returns myName.
Some errors can occur when using variables, and instead of just printing error messages, we throw exceptions. We have exceptions for three types of errors:
define method throws a MultiplyDefinedVariableException, defined in MultiplyDefinedVariableException.java.define method, the assign method throws an UndefinedVariableException, defined in UndefinedVariableException.java.eval method throws an UnassignedVariableException, defined in UnassignedVariableException.java.The classes in Sum.java, Difference.java, Product.java, and Quotient.java all perform eval by evaluating their operands and performing an operation on them. The only difference is the operator. Therefore, we have an abstract class in BinaryOp.java that has the template for evaluating a binary expression and another template for toString. These templates call abstract functions doOperation and getOperation, repectively. (The latter returns a String representation of the operator). It also has accessor methods to get the first or second expression.
Notice that evaluating an expression is really a postorder traversal of the expression tree. To evaluate a BinaryOp, first evaluate its two subtrees, and then apply the appropriate binary operator to the results of evaluating the subtrees.
Let's look at the Sum class more carefully. It provides the necessary two methods, which are fairly trivial. It supplies its deriv method, which adds the derivatives of its operands. But the interesting thing is Sum.make. Here we see the power of a factory method. It tries to simplify the expression. If the two expressions it is adding are constants, it adds them to get a new constant. If either operand is 0 it returns the other. So in three of the four cases it does not even create a Sum object! The other three operations are similar in how they try to simplify the resulting expression in their make methods.
Finally, look at the driver in ExpressionDriver.java. After the main method, we have several static wrapper methods. They alleviate the need to call the static methods in the above classes with the name of the class. We also use method names plus, minus, times, and over instead of the class names Sum, Difference, Product, and Quotient. In that way, we can construct the expression tree above using lines of code such as
Variable xVar = define("x", 2.0);
Variable yVar = define("y", 6.0);
Expression first = plus(constant(17.5), over(constant(5.0), xVar));
Expression second = minus(yVar, constant(4.0));
Expression third = times(first, second);Or we can replace the last three lines by
Expression fourth = times(plus(constant(17.5), over(constant(5.0), xVar)),
minus(yVar, constant(4.0)));The driver also verifies that the three exceptions work correctly.
This is an example of another design pattern, the composite pattern. Here we have individual things (constants and variables) and compositions of things (sums, differences, etc.), but they all are expressions and can be treated in the same manner. We perform the same operations on all of them, so we need not distinguish between individual things and groups of things. Any of the expression types can be used wherever an expression is expected, and everything works. For example, we take the derivative of the product of two huge, complicated expressions the same way that we take the derivative of 2*x.
The same pattern arises in some graphical drawing programs, where there are individual shapes (circles, rectangles, etc.) and groups of shapes (shapes are laid out and then combined into a single group). But all are shapes, and groups of shapes can be used wherever individual shapes can be used and vise versa, and all are subject to the same scaling, translation, and other operations. So you compose a bunch of shapes and get another shape.
System.err. This is not a
great solution to the problem of handling errors. Java has a much better one - exceptions.
Exceptions are objects that are thrown when an error occurs. When an exception is thrown the
program stops what it was doing and goes into error-handling mode. Exceptions are either caught
and handled in the method that throws them or passed on the the method that called it. If that method does not catch
the exception it is passed to the method that calls it, etc. If the main program does not catch the
exception it kills the program and prints an error message. You probably have seen these messages for null pointers
or subscript out of bounds.
Exceptions are an excellent way of passing an error on to a method that knows a reasonable way to handle them.
Exceptions usually occur in a low-level method. Consider trying to open a file and failing. The file-opening
method has no idea what the programmer wants to do if the file can't be opened. Maybe the method that calls
it has no idea, either. If you don't know a good way to handle the exception it is best to pass it on.
Eventually you will get to a high-level method that does know what to do about the situation. If the file
name was just entered by the user it might be good to give her a second chance. Or it may be that the
programmer has a backup file to use if the first cannot be opened. Or it could be that the right thing to
do is to print an error message and quit the program. Exceptions give a way to let the low-level method
that discovers the problem pass it on to a method that knows what to do about it.
There is a whole heirarchy of exceptions. The top level class is Exception. The heirarchy looks like:
I should also note that there are two types of exceptions, checked and unchecked.
When you call a method that could throw a checked exception the compiler checks to make sure that you
handle it. You can handle it in either of two ways. The first one is to catch it. The second is
to pass the buck and add a throws clause at the end of the method header. For example:
public String readString(String fileName) throws IOException, CloneNotSupportedException {
RunTimeException and all of its
subclasses are unchecked. The rest are checked. The checked exceptions tend to be things that
are outside of the programmers's control. The IOException exceptions happen when the file
you are reading is corrupted or there is a hardware glitch or somebody moved the file from where it
was supposed to be or gave it a different name. Since you can't control whether these things
happen you should make provisions to handle them when they do.
RunTimeException and its subclasses
are all thing that happened because you made a programming error or failed to check something
that you could have checked. The thought was that checking for all of these things is a waste
of time, and if one of them goes wrong you probably want to kill the program anyway.
(NumberFormatException is something of an exception to the rule - it often occurs
when you are trying to convert strings typed in by the user into numbers. But being unchecked
doesn't mean that you can't check for them - the compiler just doesn't check to make sure that
you do.)
So how do we catch an exception? I have modified
Fahrenheit.java to demonstrate catching
a NumberFormatException. The relevant part is in actionPerformed:
// Get the text entered in the text field.
String text = fahrenheit.getText();
try {
fahrenheitTemp = Integer.parseInt(text); // convert the text to an int
celsiusTemp = (fahrenheitTemp - 32) * 5 / 9; // do the actual conversion
// Convert the int celsius temperature to a String, and display it in
// the result label.
resultLabel.setText(Integer.toString(celsiusTemp));
}
catch(NumberFormatException ex) {
resultLabel.setText("*****");
}
The user supplies text via a fahrenheit.getText() call. However,
what the user entered may not be a valid int. Therefore we put the conversion
and the statements that deal with the result of the conversion into a try block.
If the conversion works successfully the result is displayed and the catch
block is ignored. If a NumberFormatException is thrown then catch
is called with an argument of type NumberFormatException. There can be several
catch blocks, one after another, and the first one whose parameter is of the type
of the exception (including a supertype) gets executed. Here what happens is that the output
field is filled with asteriks to show that an error occurred.
There is also another possibility - a finally block. Code in the final
block is run whether the code in the try block succeeds or fails. It is used to
clean up. A typical example is an open file that should be closed. To extend our earlier
example:
public String readString(String fileName) throws IOException {
BufferedReader input = new BufferedReader(new FileReader(pathName));
String line = input.readLine();
input.close();
return line;
}
The first line opens a file. (We will see more about file reading and writing soon.)
If an IOException is thrown by the readLine call
the file will never be closed. By rewriting it:
public String readString(String fileName) throws IOException {
BufferedReader input = new BufferedReader(new FileReader(pathName));
try {
String line = input.readLine();
}
finally {
input.close();
}
return line;
}
the file will get closed whether an exception is thrown or not. It is possible
to include both catch and finally blocks in the same
try block, but it is not recommended because of confusion over
what is happening in what order. Instead have a throws clause
(as above) or nest two try
blocks with the finally on the inside and catch on
the outside.)
Finally, you can write your own exceptions, as was done in the expression tree code. An example is
UnassignedVariableException
thrown by Variable. No exception really described the problem, so I
extended RuntimeException to create one whose name was more descriptive.