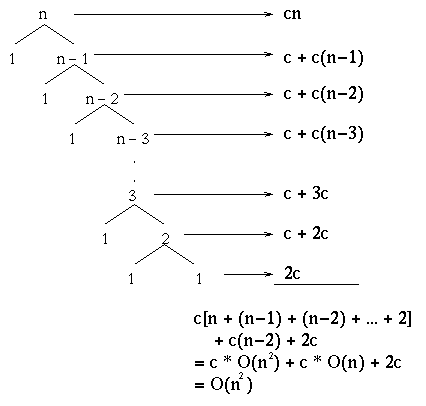
Quicksort

Quicksort runs in:

	O(n²) time in the worst case
	O(n log₂ n) time in the average case

Quicksort is a bit different than merge sort. Quicksort has good constant factors and is good in practice. It has a big advantage over merge sort in that it works in-place. It will do the sorting in the original array and a copy need not be created.

To sort a subarray A[p..r]:

Divide
- Choose an element of A[p..r].
- Call it the pivot.
- Partition A[p..r] such that:
  - A[p..q] <= pivot.
  - A[q+1..r] >= pivot.
  - Neither side of the partition has all r-p+1 elements, which is equivalent to neither side being empty. (We will see why we need this property in a moment.)
Conquer
- Recursively sort A[p..q] and A[q+1..r].
Combine
- Nothing to do.

So why must neither side of the partition have all the elements?? There are a couple of reasons:

Because then the recursive problem is the same as the original problem. Our subproblems are not getting any smaller and what we have is infinite recursion.
Furthermore, our intuition is that the subproblem sizes must always decrease in order to make progress.

In class, I put up on the board the list of numbers: 8 10 7 2 5 9 4 3. And I chose the first element as the pivot. What we ended up with was the list 3 1 4 5 2 : 7 10 9 8 6, where the colon separates the two parts of the partition. The partition is not always so even. When it is very unbalanced, quicksort ends up taking more time than merge sort.

See Demo quicksort.cpp

Let's go through some of the analysis that was done in class by looking at worst, best and average cases for quicksort. We must note though that in all the cases, to partition n elements it takes time O(n).

Worst case

The worst case in quicksort occurs when the partition gives a 1 : n-1 split every time. Graphically, this looks like:

Best case

The best case occurs when we have an even split all the time. The tree looks exactly like the recursion tree that we got for merge sort:

And as you have probably guessed by now, the running time is the same, which is O(n log₂ n).

Average case

For the average case, I will use the graceful art of handwaving. Let's just say that most splits are not too far from even. Given this, the analysis exceeds the scope of this course, but it turns out to be O(n log₂ n).

Homework #6

There are many ways in which we can choose the pivot point to almost guarantee us that our splits are not so bad. In Homework #6, we will explore how to choose the pivot point in a different way. Rather than always choosing A[p], we will choose 3 values from the array at random, and we will use the one with the middle value as the pivot by first swapping it with A[p] and then doing what we normally do to carry out quicksort. So consider this a teaser for homework #6 and maybe you will get pumped up for it!

Data Structures

Data structures by definition are ways to organize information, or data, in the computer to facilitate accessing and operating on it. However, a word of caution: It is not always obvious to what is the best way to organize that data. Here is an example of a data structure that we have seen:

Its Advantages

It is simple.
Good when elements are static or only added.
Good when <= MAXDROPS elements will never exist.
Good when we do not need to reorder elements.

Its Disadvantages

It may be too simple??
It is hard to remove elements and maintain order.
We need to know the maximum number of elements that will ever exist.
It is hard to reorder the elements.
We may waste a lot of space if the number of elements is much less than MAXDROPS.

Linked List

A linked list is a data structure in which the elements are arranged in a linear order determined by following a chain of links. Here is an example of a linked list of goalie names (you were expecting names of wingers?):

The head, tail, and next point to entire list elements, which will be implemented as objects, and not to any individual member. Also recall that "/" is the NULL character.

To Index Previous Next