

Next: Schedule
Up: Increasing the I.Q. of
Previous: Word Prediction
Analysis
Figure 4:
Simple Good-Turing smoothed 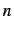 -gram probability mass
for {1,2,3}-grams. Notice how each log-log plot contains a
smooth line, masses are concentrated in lower frequencies
-gram probability mass
for {1,2,3}-grams. Notice how each log-log plot contains a
smooth line, masses are concentrated in lower frequencies 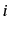 as
as
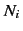 increases, and reserved probability mass increases with the
increases, and reserved probability mass increases with the
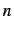 -gram size. The last point suggests larger
-gram size. The last point suggests larger 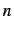 -grams are very
sparse. We do not have sufficient examples to see many new
-grams are very
sparse. We do not have sufficient examples to see many new
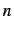 -grams, and even if we had them, grammatical correctness would
limit the number of new
-grams, and even if we had them, grammatical correctness would
limit the number of new 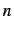 -grams.
-grams.
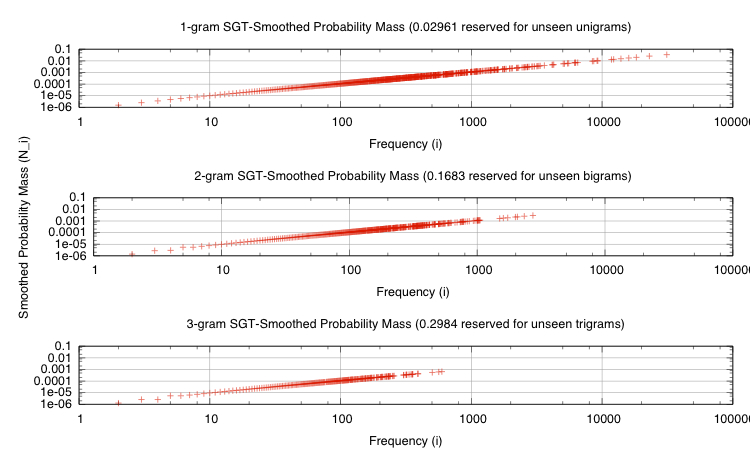 |
Figure 5:
Word prediction performance using unigrams and
bigrams. We define ``hit'' to mean a correct word prediction,
``miss'' to mean an incorrect prediction, and ``near hit'' to mean
that a matching bigram existed, but wasn't chosen because it
didn't have the highest smoothed probability. The plot depicts
the mean hit rate as
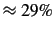 and the mean near hit rate as
and the mean near hit rate as
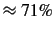 . We computed these values over our entire dataset
after smoothing
. We computed these values over our entire dataset
after smoothing  -gram probability mass using SGT.
-gram probability mass using SGT.
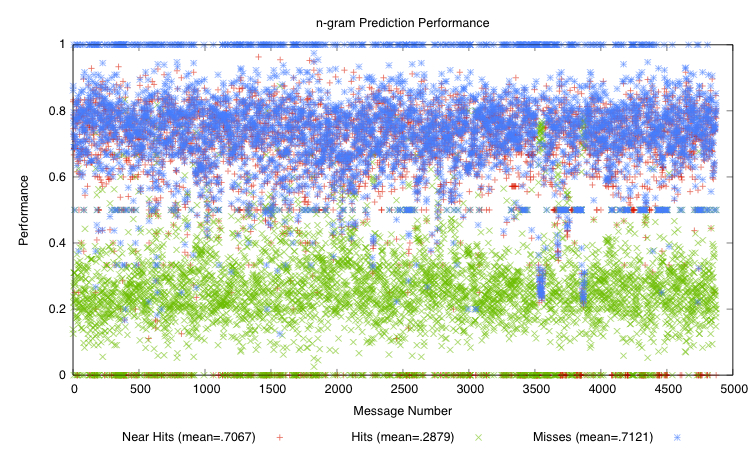 |
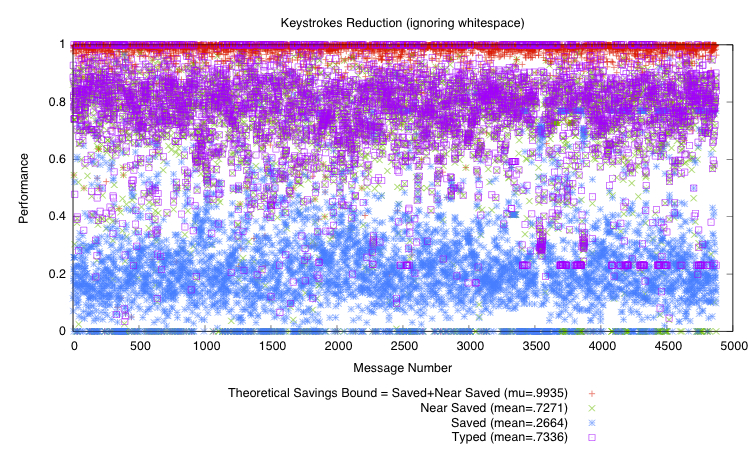
Figure 6:
Keystroke reduction using unigrams and bigrams, not
counting whitespace. We define ``saved'' to mean a correct word
prediction that eliminates typing; ``typed'' to mean characters
typed by the user because of an incorrect prediction; and ``near
saved'' to mean that a matching bigram existed, so typing could
have been avoided, but the system didn't choose the bigram because
it didn't have the highest smoothed probability. The plot depicts
the mean savings rate as
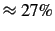 and the mean near save
rate as
and the mean near save
rate as
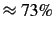 . We computed these values over our entire
dataset after smoothing
. We computed these values over our entire
dataset after smoothing  -gram probability mass using SGT. We
may find a lower ``near save'' when we split the dataset into
training and testing portions.
-gram probability mass using SGT. We
may find a lower ``near save'' when we split the dataset into
training and testing portions.
 |
Here, we apply the C-based SGT estimator to unigrams, bigrams, and
trigrams from the entire dataset and subsequently compute word
predictions using a python script.
Figure 4 depicts the probability mass associated
with each these 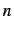 -gram dissections of the dataset,
Figure 5 shows word prediction performance using
estimators derived from unigrams and bigrams according to
equation (2), and Figure 6
shows keystroke reduction as a result of correct word prediction. We
have not yet analyzed performance after splitting data into training
and testing sets, nor have we analyzed the effects of trigrams on
prediction performance. We plan to take these steps later.
-gram dissections of the dataset,
Figure 5 shows word prediction performance using
estimators derived from unigrams and bigrams according to
equation (2), and Figure 6
shows keystroke reduction as a result of correct word prediction. We
have not yet analyzed performance after splitting data into training
and testing sets, nor have we analyzed the effects of trigrams on
prediction performance. We plan to take these steps later.
To gain a sense of performance, we have smoothed the entire dataset
and computed hits, near hits, and misses for each message. A hit is
the number of times a correct prediction is made; a near hit means
that a bigram existed, but it wasn't chosen because it did't have the
highest smoothed probability; and a miss is the number of incorrect
predictions.
Overall, the mean of bigram performance is approximately 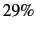 and
the mean of the near-hit rate is closer to
and
the mean of the near-hit rate is closer to 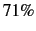 . Assessing trigram
performance, perhaps combining the two, and using context such as the
next typed letter might lead closer to the upper-bound performance
depicted in the plot. In the upper bound, we assume an ability tob
convert all near hits to hits.
. Assessing trigram
performance, perhaps combining the two, and using context such as the
next typed letter might lead closer to the upper-bound performance
depicted in the plot. In the upper bound, we assume an ability tob
convert all near hits to hits.


Next: Schedule
Up: Increasing the I.Q. of
Previous: Word Prediction
jac
2010-05-11




![]() -gram dissections of the dataset,
Figure 5 shows word prediction performance using
estimators derived from unigrams and bigrams according to
equation (2), and Figure 6
shows keystroke reduction as a result of correct word prediction. We
have not yet analyzed performance after splitting data into training
and testing sets, nor have we analyzed the effects of trigrams on
prediction performance. We plan to take these steps later.
-gram dissections of the dataset,
Figure 5 shows word prediction performance using
estimators derived from unigrams and bigrams according to
equation (2), and Figure 6
shows keystroke reduction as a result of correct word prediction. We
have not yet analyzed performance after splitting data into training
and testing sets, nor have we analyzed the effects of trigrams on
prediction performance. We plan to take these steps later.
![]() and
the mean of the near-hit rate is closer to
and
the mean of the near-hit rate is closer to ![]() . Assessing trigram
performance, perhaps combining the two, and using context such as the
next typed letter might lead closer to the upper-bound performance
depicted in the plot. In the upper bound, we assume an ability tob
convert all near hits to hits.
. Assessing trigram
performance, perhaps combining the two, and using context such as the
next typed letter might lead closer to the upper-bound performance
depicted in the plot. In the upper bound, we assume an ability tob
convert all near hits to hits.