Estimation Algorithm

To predict words, we use a statistical estimate of the next word derived from a smoothed probability distirbution over our $n$ -gram sets. We have chosen to use a version of the Good-Turing [4] estimator called Simple Good-Turing (SGT) [2] to smooth probability mass among both seen and unseen $n$ -gram values. SGT assumes the underlying distribution is binomial.

In 1995, Gale and Sampson published the Simple Good-Turing model with an algorithm, sample data, and code for the estimator [2]. Our work relies on Sampon's C code [8] and a python script we wrote to manage $n$ -grams and compute word predictions. The original Good-Turing estimator was developed by Alan Turing and an assistant I. J. Good while they worked at Beltchley Park to crack the German Enigma cipher during World War II [5].

The estimator deals with frequencies of frequencies of events and was designed to smooth a probability distribution in such a way that it accounts reasonably for events that have not occurred. A standard machine learning practice called Maximum Likelihood Estimation (MLE) does not work suitably for word prediction because it assigns probability mass solely to seen events. As we demonstrate next for unigrams, MLE neglects unseen events²:

$$P_{MLE}(w_i) = \frac{C(w_i)}{N} ,$$

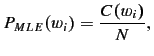
where the probability of a word $w_i$ is the count of the word $C(w_i)$ divided by the total number of words in the dataset $N$ .

Add-one or Laplace smoothing as shown in equation 1 and seen in class, adds one to estimation components to account for unseen events. Unfortunately, it takes away too much probability mass from seen events and adds to much to unseen events.

$$P_{Laplace}(w_i) = \frac{C(w_i)+1}{\sum_{j=1}^VC(w_j)+1}$$

$$= \frac{C(w_i)+1}{N+V} ,$$ (1)

where $j$ ranges across the entire vocabulatry $V$ (unique words) in the dataset.

Simple Good-Turing apportions probability mass to unseen events by using mass associated with events that occur 1 time. All events that occur $n$ times are reassigned probability mass associated with events that occur $(n-1)$ times.

To make this notion concrete, consider Table 2 which contains a sample of unigram frequencies from our dataset. If we define the total number of words in the dataset as $N=\sum iN_i$ and use Good-Turning to compute the total probability of all unseen events as $N_1/N$ , then the total probability of all unseen events in our unigram dataset is $26972/910812=.0296$ .

Table 2: Sample of unigram frequencies where $N=910812$ . Good-Turing shifts probability mass from large $N_i$ , which are better measurements, to unseen values. Note that even among the few samples shown, lower $N_i$ values clearly become noisy. This behavior is common in linguistics data.

Frequency	Frequency of Frequencies
$i$	$N_i$
1	26972
10	693
100	13
1000	0
3288	2
31262	1

The goal, then, in Good-Turing is to compute the probability for events seen $i$ times as

$$P_{GT}(w_i)=\frac{i^*}{N} .$$

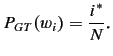
The trick is to compute $i^*$ smoothly such thtat $p_0\ne0$ as it would be using a method such as MLE (i.e., applying MLE to unseen events yields $p_0=i/N=0/N=0$ ). To do this, we rely on a theorem that states the following:

$$i^* = (i+1)\frac{\mathbb{E}\mbox{[}N_{i+1}\mbox{]}}{\mathbb{E}\mbox{[}N_i\mbox{]}} \mbox{\cite{church1991appendix}}$$

When $N_i$ is large (at lower frequencies) it represents a better measurement. In these cases, we replace $\mathbb{E}$[$N_i$] with $N_i$ and call $i^*$ a Turing estimator [3]. Small values of $N_i$ represent poor measurements with much noise, and so replacing $\mathbb{E}$[$N_i$] with $N_i$ is a poor choice. In these cases, we replace $\mathbb{E}$[$N_i$] with a smoothed estimate $S(N_i)$ as suggested by Good [4] and call $i^*$ according to the smoothing function used. Table 2 shows noise in our dataset as $i$ increases: $N_i$ oscillates at lower values.

At this point, the problem of smoothing boils down to choosing a good smoothing function and deciding when to switch between using $N_i$ and the smoothing function. For the function, we use $\log(N_i)=a+b\log(i)$ defined by Gale and Sampson [2]. The value of $b$ is learned using linear regression. Gale and Sampson call the associated Good-Turing estimate the Linear Good-Turing estimate (LGT) and a renormalized version of LGT in combination with the Turing-estimator, Simple Good-Turing (SGT). Note that once the C-code begins using the smoothing function, it continues to do so.